题目内容
(本题满分12分)
设点P在曲线 上,从原点向A(2,4)移动,如果直线OP,曲线
上,从原点向A(2,4)移动,如果直线OP,曲线 及直线x=2所围成的面积分别记为
及直线x=2所围成的面积分别记为 、
、 。
。
(Ⅰ)当 时,求点P的坐标;
时,求点P的坐标;
(Ⅱ)当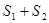 有最小值时,求点P的坐标和最小值.
有最小值时,求点P的坐标和最小值.
(1)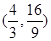 ;(2)
;(2)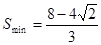 ,P点的坐标为
,P点的坐标为 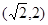 。
。
解析试题分析:(Ⅰ)设点P的横坐标为t(0<t<2),则P点的坐标为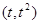 ,
,
直线OP的方程为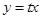 --------------2分
--------------2分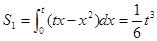 ,
,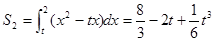 ----------6分
----------6分
因为 ,所以
,所以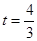 ,点P的坐标为
,点P的坐标为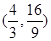 ----------7分
----------7分
(Ⅱ)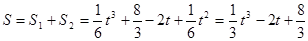 ----------8分
----------8分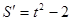 ,令S'=0得
,令S'=0得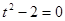 ,
,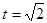 ----------9分
----------9分
因为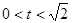 时,S'<0;
时,S'<0;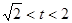 时,S'>0 ----------11分
时,S'>0 ----------11分
所以,当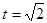 时,
时,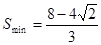 ,P点的坐标为
,P点的坐标为 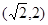 ----------12分
----------12分
考点:定积分;微积分定理;利用导数来研究函数的单调性和最值。
点评:在平常做题中,很多同学认为面积就是定积分,定积分就是面积。这里理解是错误的。实际上,我们是用定积分来求面积,但并不等于定积分就是面积。

练习册系列答案
相关题目
 ,
, 
 ,使
,使 在
在 上的最小值为
上的最小值为 ,若存在,求出
,若存在,求出 ,点P(
,点P( ,0)是函数
,0)是函数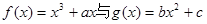 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.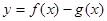 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求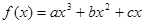 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间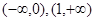 上是减函数,又
上是减函数,又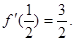
 的解析式;
的解析式;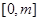 (m>0)上恒有
(m>0)上恒有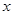 成立,求m的取值范围.
成立,求m的取值范围. (其中e为自然对数)
(其中e为自然对数) 的极值。
的极值。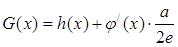 (常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。
(常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。 .
. ,求
,求 的最小值;
的最小值; ,讨论函数
,讨论函数
 R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围; ∈N*).
∈N*). ,
,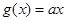 ,
,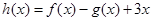 ,其中
,其中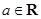 且
且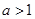 .
. 的导函数
的导函数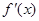 的最小值;
的最小值;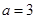 时,求函数
时,求函数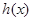 的单调区间及极值;
的单调区间及极值; ,函数
,函数 ,求实数
,求实数 的取值范围.
的取值范围.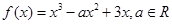
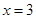 是
是 的极值点,求
的极值点,求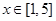 上的最大值
上的最大值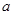 的取值范围.
的取值范围.