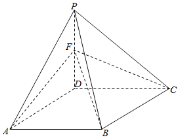
题目内容
【题目】已知抛物线![]() :
: ![]() (
(![]() )的焦点是椭圆
)的焦点是椭圆![]() :
: ![]() (
(![]() )的右焦点,且两曲线有公共点
)的右焦点,且两曲线有公共点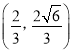
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
, ![]() ,若过点
,若过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,已知直线
两点,已知直线![]() 与
与![]() 相较于点
相较于点![]() ,试判断点
,试判断点![]() 是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
【答案】(1) ![]() (2) 点
(2) 点![]() 在定直线
在定直线![]() 上
上
【解析】试题分析:(1)由条件易得:  ,从而得到椭圆
,从而得到椭圆![]() 的方程;
的方程;
(2)先由特殊位置定出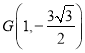 ,猜想点
,猜想点![]() 在直线
在直线![]() 上,由条件可得直线
上,由条件可得直线![]() 的斜率存在, 设直线
的斜率存在, 设直线![]() ,联立方程
,联立方程![]() ,消
,消![]() 得:
得: ![]() 有两个不等的实根,利用韦达定理转化条件即可.
有两个不等的实根,利用韦达定理转化条件即可.
试题解析:
(1)将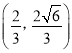 代入抛物线
代入抛物线![]() 得
得![]()
∴抛物线的焦点为![]() ,则椭圆
,则椭圆![]() 中
中![]() ,
,
又点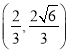 在椭圆
在椭圆![]() 上,
上,
∴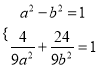 , 解得
, 解得![]() ,
,
椭圆![]() 的方程为
的方程为![]()
(2)方法一
当点![]() 为椭圆的上顶点时,直线
为椭圆的上顶点时,直线![]() 的方程为
的方程为![]() ,此时点
,此时点![]() ,
, 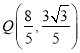 ,则直线
,则直线![]() 和直线
和直线![]() ,联立
,联立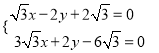 ,解得
,解得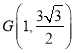 ,
,
当点![]() 为椭圆的下顶点时,由对称性知:
为椭圆的下顶点时,由对称性知:  .
.
猜想点![]() 在直线
在直线![]() 上,证明如下:
上,证明如下:
由条件可得直线![]() 的斜率存在, 设直线
的斜率存在, 设直线![]() ,
,
联立方程![]() ,
,
消![]() 得:
得: ![]() 有两个不等的实根,
有两个不等的实根,
![]() ,
, ![]()
设![]() ,则
,则![]() ,
, ![]()
则直线![]() 与直线
与直线![]()
联立两直线方程得![]() (其中
(其中![]() 为
为![]() 点横坐标)
点横坐标)
将![]() 代入上述方程中可得
代入上述方程中可得![]() ,
,
即![]() ,
,
即证![]()
将![]() 代入上式可得
代入上式可得![]()
![]() ,此式成立
,此式成立
∴点![]() 在定直线
在定直线![]() 上.
上.
方法二
由条件可得直线![]() 的斜率存在, 设直线
的斜率存在, 设直线![]()
联立方程![]() ,
,
消![]() 得:
得: ![]() 有两个不等的实根,
有两个不等的实根,
![]() ,
, ![]()
设![]() ,则
,则![]() ,
, ![]()
![]() ,
,
由![]() ,
, ![]() ,
, ![]() 三点共线,有:
三点共线,有: ![]()
由![]() ,
, ![]() ,
, ![]() 三点共线,有:
三点共线,有: ![]()
上两式相比得![]()
![]() ,
,
解得![]()
∴点![]() 在定直线
在定直线![]() 上.
上.

 名校课堂系列答案
名校课堂系列答案【题目】至2018年底,我国发明专利申请量已经连续8年位居世界首位,下表是我国2012年至2018年发明专利申请量以及相关数据.
总计 | ||||||||
年代代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 28 |
申请量 | 65 | 82 | 92 | 110 | 133 | 138 | 154 | 774 |
| 65 | 164 | 276 | 440 | 665 | 828 | 1078 | 3516 |
注:年代代码1~7分别表示2012~2018.
(1)可以看出申请量每年都在增加,请问这几年中那一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到0.01),并预测我国发明专利申请量突破200万件的年份.
的回归直线方程(精确到0.01),并预测我国发明专利申请量突破200万件的年份.
参考公式: .
.
【题目】近来天气变化无常,陡然升温、降温幅度大于![]() 的天气现象出现增多.陡然降温幅度大于
的天气现象出现增多.陡然降温幅度大于![]() 容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的
容易引起幼儿伤风感冒疾病.为了解伤风感冒疾病是否与性别有关,在某妇幼保健院随机对人院的![]() 名幼儿进行调查,得到了如下的列联表,若在全部
名幼儿进行调查,得到了如下的列联表,若在全部![]() 名幼儿中随机抽取
名幼儿中随机抽取![]() 人,抽到患伤风感冒疾病的幼儿的概率为
人,抽到患伤风感冒疾病的幼儿的概率为![]() ,
,
(1)请将下面的列联表补充完整;
患伤风感冒疾病 | 不患伤风感冒疾病 | 合计 | |
男 | 25 | ||
女 | 20 | ||
合计 | 100 |
(2)能否在犯错误的概率不超过![]() 的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
的情况下认为患伤风感冒疾病与性别有关?说明你的理由;
(3)已知在患伤风感冒疾病的![]() 名女性幼儿中,有
名女性幼儿中,有![]() 名又患黄痘病.现在从患伤风感冒疾病的
名又患黄痘病.现在从患伤风感冒疾病的![]() 名女性中,选出
名女性中,选出![]() 名进行其他方面的排查,记选出患黄痘病的女性人数为
名进行其他方面的排查,记选出患黄痘病的女性人数为![]() ,求
,求![]() 的分布列以及数学期望.下面的临界值表供参考:
的分布列以及数学期望.下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: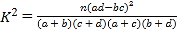 ,其中
,其中![]()
【题目】某茶楼有四类茶饮,假设为顾客准备泡茶工具所需的时间互相独立,且都是整数分钟,经统计以往为100位顾客准备泡茶工具所需的时间![]() ,结果如下:
,结果如下:
类别 | 铁观音 | 龙井 | 金骏眉 | 大红袍 |
顾客数(人) | 20 | 30 | 40 | 10 |
时间 | 2 | 3 | 4 | 6 |
注:服务员在准备泡茶工具时的间隔时间忽略不计,并将频率视为概率.
(1)求服务员恰好在第6分种开始准备第三位顾客的泡茶工具的概率;
(2)用![]() 表示至第4分钟末已准备好了工具的顾客人数,求
表示至第4分钟末已准备好了工具的顾客人数,求![]() 的分布列及数学期望.
的分布列及数学期望.