题目内容
2.已知正整数a,b满足4a+b=30,使得$\frac{1}{a}$+$\frac{1}{b}$取最小值时,则实数对(a,b)是( )| A. | (5,10) | B. | (6,6) | C. | (10,5) | D. | (7,2) |
分析 利用4a+b=30与$\frac{1}{a}$+$\frac{1}{b}$相乘,展开利用均值不等式求解即可.
解答 解:∵正数a,b满足4a+b=30,
∴$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{30}$(4a+b)($\frac{1}{a}$+$\frac{1}{b}$)
=$\frac{1}{30}$(4+1+$\frac{b}{a}$+$\frac{4a}{b}$)≥$\frac{3}{10}$,
当且仅当$\frac{b}{a}$=$\frac{4a}{b}$,即当a=5,b=10时等号成立.
故选:A.
点评 利用基本不等式求函数最值是高考考查的重点内容,对不符合基本不等式形式的应首先变形,然后必须满足三个条件:一正、二定、三相等.同时注意灵活运用“1”的代换.

练习册系列答案
相关题目
13.过点M(1,2),N(m,3)的直线与2x-3y+1=0垂直,则m的值为( )
| A. | 1 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | -1 |
12.将2名教师,6名学生分成两个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由1名教师3名学生组成,不同的安排方案共有( )
| A. | 10 | B. | 40 | C. | 20 | D. | 不能确定 |
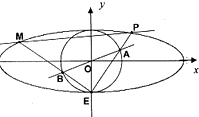 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=b2,已知椭圆C1过点(1,$\frac{\sqrt{2}}{2}$),焦距为2.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和圆C2:x2+y2=b2,已知椭圆C1过点(1,$\frac{\sqrt{2}}{2}$),焦距为2.