Question

15．已知复数z的实部为整数，且2z•$\overline{z}$-z=$\frac{10}{3+i}$
（1）求复数z；
（2）若复数u满足|u+2|=|z|，求|u|的取值范围．

Answer 1

分析 （1）设z=a+bi（a∈z，b∈R），代入2z•$\overline{z}$-z=$\frac{10}{3+i}$，整理后由复数相等的条件列方程组求得a，b的值得答案；
（2）求出|z|=$\sqrt{2}$，代入|u+2|=|z|，数形结合求得|u|的取值范围．

解答 解：（1）设z=a+bi（a∈z，b∈R），
代入2z•$\overline{z}$-z=$\frac{10}{3+i}$，得$2（{a}^{2}+{b}^{2}）-a-bi=\frac{10（3-i）}{（3+i）（3-i）}=\frac{10（3-i）}{10}=3-i$，
∴$\left\{\begin{array}{l}{2{a}^{2}+2{b}^{2}-a=3}\\{b=1}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=1}\\{b=1}\end{array}\right.$或$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\end{array}\right.$（舍）．
∴z=1+i；
（2）∵z=1+i，∴|z|=$\sqrt{2}$，
则|u+2|=|z|=$\sqrt{2}$，
∴复数u在复平面内对应的点的轨迹如图，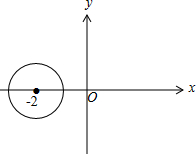

∴|u|的取值范围是[2-$\sqrt{2}$，2+$\sqrt{2}$]．

点评 本题考查复数代数形式的混合运算，考查复数模的几何意义，体现了数形结合的解题思想方法，是基础题．