题目内容
已知圆x2+y2-6x-7=0与抛物线y2="2px" (p>0)的准线相切,则p=__ __.
2
解:圆方程:x2+y2-6x-7=0化为:(x-3)2+y2=16,
垂直于x轴的切线为:x=-1,x=7.
抛物线y2=2px(p>0)的准线方程为x="-p" /2 ,
因为抛物线y2=2px(p>0)的准线与圆(x-3)2+y2=16相切,
所以 -p/2 =-1,解得p=2
故答案为:2
垂直于x轴的切线为:x=-1,x=7.
抛物线y2=2px(p>0)的准线方程为x="-p" /2 ,
因为抛物线y2=2px(p>0)的准线与圆(x-3)2+y2=16相切,
所以 -p/2 =-1,解得p=2
故答案为:2

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
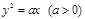 ,直线l与抛物线交于A、B,且
,直线l与抛物线交于A、B,且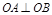 ,点
,点 在AB上,又
在AB上,又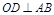 .
.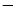 2,过P,Q分别作抛物线的切线,两切线交于点A,则点A的纵坐标为
2,过P,Q分别作抛物线的切线,两切线交于点A,则点A的纵坐标为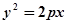 的准线
的准线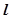 ,焦点为
,焦点为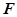 ,顶点为
,顶点为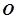 ,
,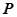 为抛物线上任意一点,
为抛物线上任意一点,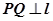 ,
,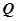 为垂足,求
为垂足,求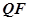 与
与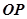 的交点
的交点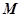 的轨迹方程.
的轨迹方程.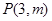 在以点
在以点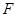 为焦点的抛物线
为焦点的抛物线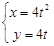 (
(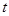 为参数)上,则
为参数)上,则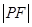 等于( )
等于( ) 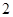
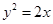 的焦点
的焦点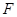 作直线交抛物线于
作直线交抛物线于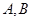 两点,若
两点,若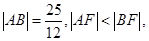 则
则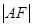 = 。
= 。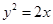 ,过动点
,过动点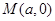 且斜率为1的直线
且斜率为1的直线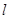 与抛物线交于不同两点A、B,|AB|
与抛物线交于不同两点A、B,|AB|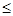 2.
2.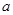 的取值范围;
的取值范围;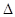 NAB面积的最大值.
NAB面积的最大值.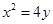 的焦点坐标为_________
的焦点坐标为_________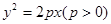 的焦点为
的焦点为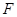 ,过点
,过点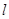 与抛物线交于
与抛物线交于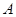 、
、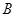 两点,抛物线的准线与
两点,抛物线的准线与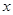 轴交于点
轴交于点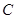 .
.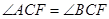 ;
;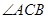 的最大值,并求
的最大值,并求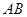 的长.
的长.