题目内容
设函数 ,
, ,其中实数
,其中实数 .
.
(1)若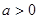 ,求函数
,求函数 的单调区间;
的单调区间;
(2)当函数 与
与 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 的最小值为
的最小值为 ,求
,求 的值域;
的值域;
(3)若 与
与 在区间
在区间 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.
 ,
, ,其中实数
,其中实数 .
.(1)若
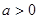 ,求函数
,求函数 的单调区间;
的单调区间;(2)当函数
 与
与 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 的最小值为
的最小值为 ,求
,求 的值域;
的值域;(3)若
 与
与 在区间
在区间 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.(1)详见解析;(2)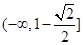 ;(3)
;(3)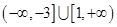 .
.
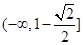 ;(3)
;(3)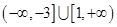 .
.试题分析:(1)这是一个三次函数求单调区间的问题,此类问题比较熟悉,三次函数的导数为二次函数,它的零点容易求出,但要注意对零点大小的比较,才能准确写出单调区间;(2)函数
 与
与 的图象只有一个公共点,知方程
的图象只有一个公共点,知方程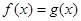 只有一个根(含重根),结合
只有一个根(含重根),结合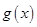 有最小值,可求出
有最小值,可求出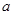 的取值范围,而
的取值范围,而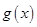 是一个二次函数,易得它提最小值
是一个二次函数,易得它提最小值 ,最后可求出
,最后可求出 的值域;(3)由(1)的过程和结果易知
的值域;(3)由(1)的过程和结果易知 的单调增区间,
的单调增区间, 应是其子区间,再由
应是其子区间,再由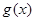 的单调增区间,
的单调增区间, 也应是其子区间,从而确定
也应是其子区间,从而确定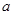 的取值范围,要注意分类讨论思想的应用.
的取值范围,要注意分类讨论思想的应用.试题解析:(1)∵
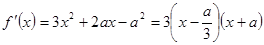 ,又
,又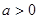
∴当
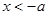 或
或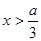 时,
时,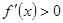 ;当
;当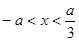 时,
时,
∴
 的递增区间为
的递增区间为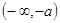 和
和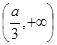 ,递减区间为
,递减区间为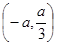 .
.(2)由题意知
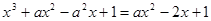
即
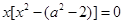 恰有一根(含重根)∴
恰有一根(含重根)∴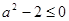 ,即
,即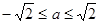 ,
,又
 ,且
,且 存在最小值,所以
存在最小值,所以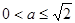
又
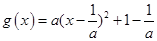 ,∴
,∴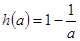 ,∴
,∴ 的值域为
的值域为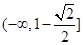 .
.(3)当
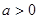 时,
时, 在
在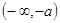 和
和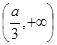 内是增函数,
内是增函数, 在
在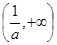 内是增函数,由题意得
内是增函数,由题意得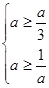 ,解得
,解得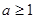 .
.当
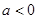 时,
时, 在
在 和
和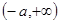 内是增函数,
内是增函数, 在
在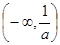 内是增函数,由题意得
内是增函数,由题意得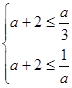 ,解得
,解得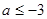 .
.综上可知,实数
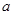 的取值范围为
的取值范围为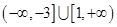 .
.
练习册系列答案
相关题目
 毫克)与时间
毫克)与时间 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后, 的函数关系式为
的函数关系式为 (
( 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题:
 ,则股价
,则股价 (元)和时间
(元)和时间 的关系在
的关系在 段可近似地用解析式
段可近似地用解析式 来描述,从
来描述,从 点走到今天的
点走到今天的 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且 :
: 对称。老张预计这只股票未来的走势如图中虚线所示,这里
对称。老张预计这只股票未来的走势如图中虚线所示,这里 段与
段与 段是股价延续
段是股价延续
 。现在老张决定取点
。现在老张决定取点
 ,点
,点 ,点
,点 来确定解析式中的常数
来确定解析式中的常数 ,
,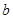 ,
, ,
, ,并且求得
,并且求得 。
。 .
. 为何实数,
为何实数, 总是增函数;
总是增函数;
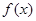 是定义在
是定义在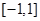 上的奇函数,且
上的奇函数,且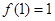 ,若
,若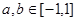 ,
,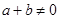 有
有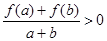 恒成立.
恒成立.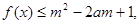 对所有
对所有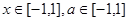 恒成立,求实数
恒成立,求实数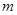 的取值范围。
的取值范围。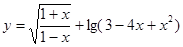 的定义域为
的定义域为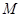 ,
,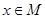 时,求
时,求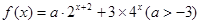 的最小值.
的最小值.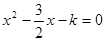 在(-1,1)上有实根,则
在(-1,1)上有实根,则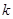 的取值范围为( )
的取值范围为( )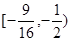
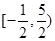
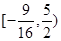
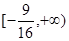
 ,其中
,其中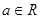 ,若对任意的非零实数
,若对任意的非零实数 ,存在唯一的非零实数
,存在唯一的非零实数 ,使得
,使得 成立,则k的最小值为( )
成立,则k的最小值为( )