题目内容
6．
求经过棱长为1的正方体ABCD-A1B1C1D1的棱AA1和CC1的中点E、F及点D1的截面，并求截面与正方体的下底面以及正方体侧面所围成的几何体的体积．
分析 连接D1E，D1F，BE，BF，则四边形D1EBF即为符合要求的截面，故截面与正方体的下底面以及正方体侧面所围成的几何体的体积为正方体体积的一半．
解答 解：连接D1E，D1F，BE，BF，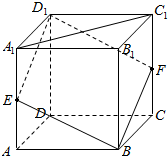
∵E，F是A1A，C1C的中点，
∴D1E∥BF，且D1E=BF，
∴平行四边形D1EBF即为符合要求的截面．
根据正方体的对称性可得截面与正方体的下底面以及正方体侧面所围成的几何体的体积为正方体体积的一半．
∴V=$\frac{1}{2}$．
点评 本题考查了平面的性质及空间几何体的体积计算，找到截面上下两部分体积相等是解题关键．
练习册系列答案
走进文言文系列答案
相关题目
16．在区间（10，20]内的所有实数中随机取一个实数a，则这个实数a＞17的概率是（ ）
| A． | $\frac{7}{10}$ | B． | $\frac{3}{10}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{7}$ |
17．抛物线y=2x2的焦点坐标是（ ）
| A． | （0，$\frac{1}{2}$） | B． | （$\frac{1}{2}$，0） | C． | （0，$\frac{1}{8}$） | D． | （$\frac{1}{8}$，0） |
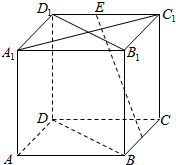在正方体ABCD-A1B1C1D1中，E，F分别为C1D1，BC的中点