题目内容
11.已知M(-1,2)为椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{16}$=1内一点,直线l过点M,交椭圆于A,B两点,且M为弦AB的中点,求l的方程.分析 设以点M(-1,2)为中点的弦与椭圆交于A(x1,y1),B(x2,y2),利用点差法能求出结果.
解答 解:设以点M(-1,2)为中点的弦与椭圆交于A(x1,y1),B(x2,y2),
则x1+x2=-2,y1+y2=4,
分别把M(x1,y1),N(x2,y2)代入椭圆方程$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{16}$=1,
可得$\frac{{{x}_{1}}^{2}}{4}+\frac{{{y}_{1}}^{2}}{16}=1$,$\frac{{{x}_{2}}^{2}}{4}+\frac{{{y}_{2}}^{2}}{16}=1$.
再相减可得(x1+x2)(x1-x2)+$\frac{1}{4}$(y1+y2)(y1-y2)=0,
∴-2(x1-x2)+(y1-y2)=0,
∴k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=2,
∴点M(-1,2)为中点的弦所在直线方程l的方程为:y-2=2(x+1),
整理,得:2x-y+4=0.
所求直线方程为:2x-y+4=0.
点评 本题考查直线方程的求法,直线与椭圆的位置关系的综合应用,是中档题,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
1.已知$\overrightarrow{a}$=(1,sinα),$\overrightarrow{b}$=(cos2α,2sinα-1),α∈($\frac{π}{2}$,π).若$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{5}$,则tan(α+$\frac{π}{4}$)的值为( )
| A. | $\frac{2}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{7}$ | D. | -$\frac{1}{7}$ |
19.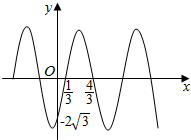 已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则下列判断错误的是( )
 已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则下列判断错误的是( )| A. | 函数f(x)的最小正周期为2 | |
| B. | 函数f(x)的值域为[一4,4] | |
| C. | 函数f(x)的图象关于( $\frac{10}{3}$,0)对称 | |
| D. | 函数f(x)的图象向左平移 $\frac{π}{3}$个单位后得到y=Asinωx的图象 |
20.下列各对向量中,共线的是( )
| A. | $\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(3,-2) | B. | $\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(4,-6) | C. | $\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=($\sqrt{3}$,3) | D. | $\overrightarrow{a}$=(4,7),$\overrightarrow{b}$=(7,4) |
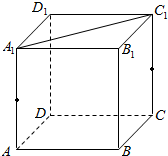 求经过棱长为1的正方体ABCD-A1B1C1D1的棱AA1和CC1的中点E、F及点D1的截面,并求截面与正方体的下底面以及正方体侧面所围成的几何体的体积.
求经过棱长为1的正方体ABCD-A1B1C1D1的棱AA1和CC1的中点E、F及点D1的截面,并求截面与正方体的下底面以及正方体侧面所围成的几何体的体积.