题目内容
15.已知直线y=$\sqrt{3}$(x-2)与抛物线C:y2=8x相交于A,B两点,点F为C的焦点,若$\overrightarrow{AF}$=$λ\overrightarrow{FB}$(|$\overrightarrow{AF}$|>|$\overrightarrow{FB}$|)则λ=3.分析 设出A,B的坐标,利用向量条件,可得λ=-$\frac{{y}_{1}}{{y}_{2}}$,联立直线方程与抛物线方程,解得答案.
解答 解:根据题意设A(x1,y1),B(x2,y2),
由$\overrightarrow{AF}$=$λ\overrightarrow{FB}$(|$\overrightarrow{AF}$|>|$\overrightarrow{FB}$|),可得y1>y2,
且(2-x1,-y1)=λ(x2-2,y2),故-y1=λy2,
∴λ=-$\frac{{y}_{1}}{{y}_{2}}$,
联立直线与抛物线方程,$\left\{\begin{array}{l}y=\sqrt{3}(x-2)\\{y}^{2}=8x\end{array}\right.$,消元得:y2-$\frac{8\sqrt{3}}{3}$y-16=0,
解得:y1=$4\sqrt{3}$,y2=-$\frac{4\sqrt{3}}{3}$,
∴λ=3.
故答案为:3
点评 本题考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.已知函数f(x)=x2+(a+8)x+a2+a-12,且f(a2-4)=f(2a-8),设等差数列{an}的前n项和为Sn,(n∈N*)若Sn=f(n),则$\frac{{S}_{n}-4a}{{a}_{n}-1}$的最小值为( )
| A. | $\frac{27}{6}$ | B. | $\frac{35}{8}$ | C. | $\frac{14}{3}$ | D. | $\frac{37}{8}$ |
20.下列各对向量中,共线的是( )
| A. | $\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(3,-2) | B. | $\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(4,-6) | C. | $\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=($\sqrt{3}$,3) | D. | $\overrightarrow{a}$=(4,7),$\overrightarrow{b}$=(7,4) |
4.函数y=$\sqrt{2}$sin2x是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶 |
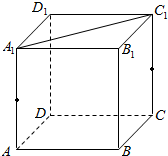 求经过棱长为1的正方体ABCD-A1B1C1D1的棱AA1和CC1的中点E、F及点D1的截面,并求截面与正方体的下底面以及正方体侧面所围成的几何体的体积.
求经过棱长为1的正方体ABCD-A1B1C1D1的棱AA1和CC1的中点E、F及点D1的截面,并求截面与正方体的下底面以及正方体侧面所围成的几何体的体积.