题目内容
16．在△ABC中，已知a：b：c=3：5：4，则△ABC最大角的余弦值为0．分析 根据题意，a：b：c=3：5：4，可以设a=3t，b=5t，c=4t，则b为最大边，∠B为最大角，由余弦定理计算可得cosB的值，即可得答案．
解答 解：根据题意，a：b：c=3：5：4，可以设a=3t，b=5t，c=4t，
则b为最大边，∠B为最大角，
则cosB=$\frac{（3t）^{2}+（4t）^{2}-（5t）^{2}}{2（3t）（4t）}$=0；
故△ABC最大角的余弦值为0；
故答案为：0．
点评 本题考查余弦定理的运用，关键是由正弦定理分析出三角形的三边的关系．
练习册系列答案
相关题目
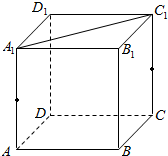求经过棱长为1的正方体ABCD-A1B1C1D1的棱AA1和CC1的中点E、F及点D1的截面，并求截面与正方体的下底面以及正方体侧面所围成的几何体的体积．
4．函数y=$\sqrt{2}$sin2x是（ ）
| A． | 奇函数 | B． | 偶函数 | ||
| C． | 既是奇函数又是偶函数 | D． | 非奇非偶 |