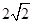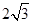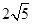题目内容
以直线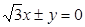
为渐近线，一个焦点坐标为
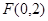的双曲线方程是（ ）
A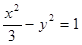． | B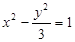． | C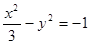． | D． |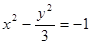
D
解析试题分析：一个焦点坐标为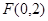，说明双曲线的焦点在
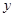轴上.因为渐近线方程为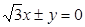，所以可设双曲线方程为
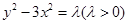，即
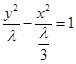，所以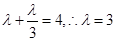
，所以双曲线方程为.
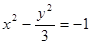考点：本小题主要考查双曲线标准方程的求法，考查学生分析问题、解决问题的能力和求解运算能力.
点评：已知双曲线的渐近线方程求双曲线的标准方程可以采取题目中所用的方法，可以简化运算，但是只有双曲线的渐近线方程并不能确定双曲线的焦点在哪个坐标轴上，所以并不能确定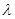
的正负.
练习册系列答案
相关题目
短轴长为
，离心率为
的椭圆的两个焦点分别为F1，F2，过F1作直线交椭圆于A，B两点，则△ABF2的周长为
| A．24 | B．12 | C．6 | D．3 |
为抛物线
的焦点，
为抛物线上三点．
为坐标原点，若是
的重心,
的面积分别为
3，则
＋
＋
的值为: ( )
| A．3 | B．4 | C．6 | D．9 |
设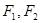
是椭圆
的两个焦点，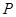
是椭圆上的点，且
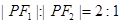，则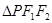
的面积为（ ）
| A．4 | B．6 | C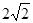． | D． |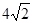
，则方程
表示的曲线不可能是（ ）
| A．圆 | B．椭圆 | C．双曲线 | D．抛物线 |
已知点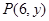
在抛物线
上，
为抛物线焦点， 若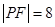
, 则点到抛物线准线的距离等于（ ）
| A．2 | B．1 | C．4 | D．8 |
设点
是曲线
上的点，
，则（ ）
A． | B． |
C． | D． |
已知双曲线
的一个焦点与抛物线
的焦点重合，且双曲线的离心率等于
，则该双曲线的标准方程为（ ）
A． | B． |
C． | D． |
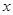轴对称，它的顶点在坐标原点
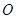，并且经过点
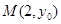.若点
到该抛物线焦点的距离为
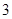，则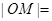
（ ）
