题目内容
短轴长为 ,离心率为
,离心率为 的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为
的椭圆的两个焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为
| A.24 | B.12 | C.6 | D.3 |
B
解析试题分析:由已知中短轴长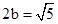 ,和离心率
,和离心率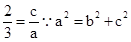 的值得到参数a,b,c的值,分别是a=3,b=2,然后结合题中条件得到三角形△ABF2的周长为椭圆上点到两焦点的距离和的2倍,故为4a=12,进而求解选B
的值得到参数a,b,c的值,分别是a=3,b=2,然后结合题中条件得到三角形△ABF2的周长为椭圆上点到两焦点的距离和的2倍,故为4a=12,进而求解选B
考点:本题主要考查了椭圆几何量之间的关系,利用了椭圆的定义,属于基础题.
点评:解决该试题的关键是分析出所求解的三角形的三边两边的和是符合椭圆的定义的,另一边是焦距,这样可以求解得到。

练习册系列答案
相关题目
椭圆 上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于 的等差数列, 则n的最大值是( )
的等差数列, 则n的最大值是( )
| A.198 | B.199 | C.200 | D.201 |
与椭圆 共焦点且过点
共焦点且过点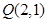 的双曲线方程是( )
的双曲线方程是( )
A.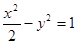 | B. |
C. | D.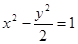 |
曲线 与曲线
与曲线 的( )
的( )
| A.长轴长相等 | B.短轴长相等 | C.离心率相等 | D.焦距相等 |
如图所示,A,B,C分别为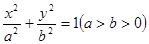 的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )
的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )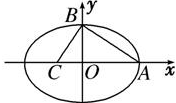
A.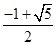 | B.1-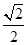 | C.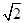 -1 -1 | D.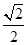 |
双曲线 的焦点坐标为
的焦点坐标为
A. | B. | C. | D. |
以直线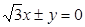 为渐近线,一个焦点坐标为
为渐近线,一个焦点坐标为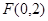 的双曲线方程是( )
的双曲线方程是( )
A.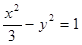 | B.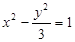 | C.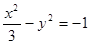 | D.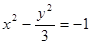 |
 、
、 是双曲线
是双曲线 的两焦点,点
的两焦点,点 在该双曲线上,且
在该双曲线上,且 是等腰三角形,则
是等腰三角形,则






