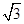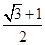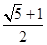题目内容
 为抛物线
为抛物线 的焦点,
的焦点, 为抛物线上三点.
为抛物线上三点. 为坐标原点,若
为坐标原点,若 是
是 的重心,
的重心, 的面积分别为
的面积分别为 3,则
3,则 +
+ +
+ 的值为: ( )
的值为: ( )
| A.3 | B.4 | C.6 | D.9 |
A
解析试题分析:设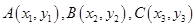 ,因为
,因为 为抛物线上三点,所以
为抛物线上三点,所以
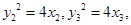
 为抛物线
为抛物线 的焦点,所以
的焦点,所以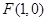 ,因为
,因为 是
是 的重心,所以
的重心,所以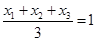 ,即
,即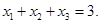
所以 +
+ +
+
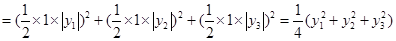
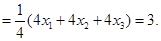
考点:本小题主要考查抛物线的标准方程、抛物线上点的性质、重心坐标公式及三角形面积公式的应用,考查学生综合分析问题、解决问题的能力,考查学生的运算求解能力.
点评:截距此类问题时,要注意“设而不求”思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
双曲线 的焦点坐标为
的焦点坐标为
A. | B. | C. | D. |
椭圆 的焦点为F1和F2 ,点P在椭圆上,如果线段PF1的中点在y轴上,那么︱PF1︱是︱PF2︱
的焦点为F1和F2 ,点P在椭圆上,如果线段PF1的中点在y轴上,那么︱PF1︱是︱PF2︱
| A.3倍 | B.4倍 | C.5倍 | D.7倍 |
双曲线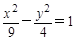 与直线
与直线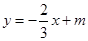 (
(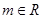 )的公共点的个数为( ).
)的公共点的个数为( ).
| A.0 | B.1 | C.0或1 | D.0或1或2 |
已知椭圆的中心在原点,焦点在x轴上,且长轴长为 ,离心率为
,离心率为 ,则椭圆的方程是( )
,则椭圆的方程是( )
A. + + =1 =1 | B. + + =1 =1 | C. + + =1 =1 | D. + + =1 =1 |
以直线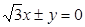 为渐近线,一个焦点坐标为
为渐近线,一个焦点坐标为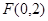 的双曲线方程是( )
的双曲线方程是( )
A.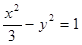 | B.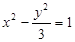 | C.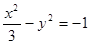 | D.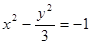 |
双曲线 的离心率为
的离心率为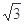 ,则它的渐近线方程是( )
,则它的渐近线方程是( )
A.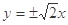 | B.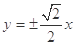 | C.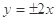 | D.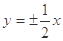 |




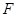 ;虚轴的—个端点为
;虚轴的—个端点为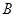 ,如果直线
,如果直线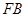 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )