题目内容
【题目】如图,已知四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 为
为![]() 上任意一点,
上任意一点,![]() 为菱形
为菱形![]() 对角线的交点。
对角线的交点。
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,当四棱锥的体积被平面
,当四棱锥的体积被平面![]() 分成3:1两部分时,若二面角
分成3:1两部分时,若二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值。
的值。

【答案】(1)见解析(2)![]()
【解析】
(1)通过在面内作交线的垂线,和面面垂直性质定理证明![]() 面ABCD,再通过
面ABCD,再通过![]() 面PDB,证明平面
面PDB,证明平面![]() 平面
平面![]() 。(2)设三棱锥
。(2)设三棱锥![]() 的高为
的高为![]() ,由体积比可得
,由体积比可得![]() ,故此时
,故此时![]() 为
为![]() 的中点。可证面
的中点。可证面![]() 面
面![]() 。过点
。过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,故
,故![]() 即为二面角
即为二面角![]() 的平面角,即
的平面角,即![]() 。进一步求的
。进一步求的![]() 的值。方法二是利用空量向量求得比值。
的值。方法二是利用空量向量求得比值。
(1)过点![]() 作
作![]() 于点G,由于平面
于点G,由于平面![]() 面
面![]() ,所以
,所以![]() 面
面![]()
![]() 面
面![]() ,故
,故![]() ;同理,过点
;同理,过点![]() 作
作![]() 于
于![]() ,则
,则![]()
![]() 面
面![]() ,
,![]() 面
面![]() ,且
,且![]()
所以![]() 面ABCD。所以
面ABCD。所以![]() ,又
,又![]() ,
,
故![]() 面
面![]() ,所以面
,所以面![]() 面面
面面![]() 。
。
(2)若四棱锥的体积被面![]() 分成3:1两部分,则
分成3:1两部分,则![]() 的体积是整个四棱锥体积的
的体积是整个四棱锥体积的![]() ,设三棱锥
,设三棱锥![]() 的高为
的高为![]() ,则
,则![]() (
(![]() 为菱形
为菱形![]() 的面积),所以
的面积),所以![]() ,故此时
,故此时![]() 为
为![]() 的中点,此时
的中点,此时![]() ,并且
,并且![]() ,故面
,故面![]() 面
面![]() ,故
,故![]() 面
面![]() ,
,![]() ,
,
过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 面
面![]() ,连接
,连接![]() ,则
,则![]() ,故
,故![]() 即为二面角
即为二面角![]() 的平面角,即
的平面角,即![]()

设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,故
,故![]() ,
,![]()
可解得![]() ,故
,故![]()
解法二:如图建立坐标系,设![]() 则
则![]() ,设
,设![]()
则![]()
面![]() 的法向量为
的法向量为![]() ,设面面
,设面面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,取
,取![]() ,则
,则
![]()
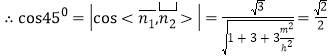
![]()

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
【题目】全国糖酒商品交易会将在四川举办.展馆附近一家川菜特色餐厅为了研究参会人数与本店所需原材料数量的关系,在交易会前查阅了最近5次交易会的参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下数据:
(袋),得到如下数据:
举办次数 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
参会人数 | 11 | 9 | 8 | 10 | 12 |
原材料 | 28 | 23 | 20 | 25 | 29 |
(Ⅰ)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)若该店现有原材料12袋,据悉本次交易会大约有13万人参加,为了保证原材料能够满足需要,则该店应至少再补充原材料多少袋?
(参考公式: ,
,![]() )
)


