题目内容
【题目】设抛物线![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,抛物线的焦点
,抛物线的焦点![]() ,以
,以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆与抛物线的一个交点为
的椭圆与抛物线的一个交点为 ;自
;自![]() 引直线交抛物线于
引直线交抛物线于![]() 两个不同的点,设
两个不同的点,设![]() .
.
(1)求抛物线的方程椭圆的方程;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
, ![]() (2)
(2)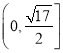
【解析】分析:(1)根据已知分别列方程组求标准方程中的待定系数即可. (2)先利用弦长公式计算出
![]()
![]() ,再求函数的值域,即得
,再求函数的值域,即得![]() 的取值范围.
的取值范围.
详解: (1)设椭圆的标准方程为![]() ,
,
由题意得 ,解得
,解得![]()
∴椭圆的方程为![]()
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,∴抛物线的方程是
,∴抛物线的方程是![]()
(2)由题意得直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() ,
,
由![]() 消去
消去![]() 整理得
整理得![]() (*)
(*)
∵直线![]() 与抛物线交于两点,
与抛物线交于两点,
∴![]() ,
,
设![]() ,则
,则![]() ①,
①,![]() ②,
②,
∵![]() ,
, ![]()
∴![]()
∴![]() ,③
,③
由①②③消去![]() 得
得![]() .
.
∴![]()
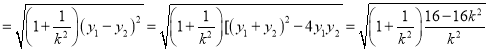
![]() ,即
,即![]()
![]() ,将
,将![]() 代入上式得,
代入上式得,
![]()
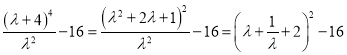 ,
,
∵![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() ,
,
∴![]()
![]() ,
,
∴![]() ,即
,即![]() 的取值范围为
的取值范围为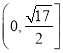 .
.

练习册系列答案
相关题目


