Question

【题目】如图，四棱柱的底面是正方形，为和的交点，

若。

（1）求证：平面；

（2）求二面角的余弦值。

Answer 1

【答案】（1）见解析；（2）

【解析】分析：第一问把握题中的条件，挖掘有用的信息，找到垂直的条件，应用线面垂直的判定定理证得结果，第二问利用空间向量求二面角，先根据垂直关系，建立相应的空间直角坐标系，求出面的法向量，利用数量积与模求得余弦值，最后结合法向量的方向确定最后的结果.

详解：（1）证明：连接，

由题意知均是边长为2的等边三角形，

所以 ，所以。

因为底面是正方形，所以与垂直平分于点，

所以，且，

因为，所以，

因为平面，所以平面。

（2）由（1）可知平面，所以，

所以为二面角的平面角，

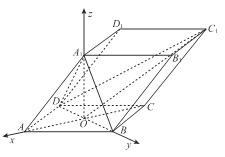
以为原点，建立空间直角坐标系，如图，

则，

所以，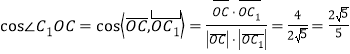

所以二面角的余弦值为。