Question

【题目】已知函数f（x）=x3+ax2+bx+1在x=﹣1与x=2处有极值．
（1）求函数f（x）的解析式；
（2）求f（x）在[﹣2，3]上的最值．

Answer 1

【答案】
（1）解：f′（x）=3x2+2ax+b，

∵函数f（x）=x3+ax2+bx+1在x=﹣1与x=2处有极值，

∴﹣1，2是f′（x）=0的两个实数根，

∴ ，解得 ．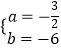

∴f（x）=

（2）解：由（1）可得f′（x）=3x2﹣3x﹣6=3（x﹣2）（x+1）．

利用f′（x）=0，解得x=﹣1，2．

列出表格：

x	[﹣2，﹣1）	﹣1	（﹣1，2）	2	（2，3]
f′（x）	+	0	﹣	0	+
f（x）	单调递增	极大值	单调递减	极小值	单调递增

由表格可知：当x=﹣1时，函数f（x）取得极大值，f（﹣1）= ；当x=2时，函数f（x）取得极小值，f（2）=﹣9．又f（﹣2）=﹣1，f（3）=﹣ ．

可得：当x=﹣1时，函数f（x）取得最大值 ；当x=2时，函数f（x）取得最小值﹣9

【解析】（1）f′（x）=3x2+2ax+b，由于函数f（x）=x3+ax2+bx+1在x=﹣1与x=2处有极值，可知﹣1，2是f′（x）=0的两个实数根，代入即可解出；（2）由（1）可得f′（x）=3x2﹣3x﹣6=3（x﹣2）（x+1）．利用f′（x）=0，解得x=﹣1，2．列出表格：即可得出极值与区间端点的函数值，经过比较即可得出最值．
【考点精析】本题主要考查了函数的极值与导数和函数的最大(小)值与导数的相关知识点，需要掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值；求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．