��Ŀ����
����Ŀ����14�֣���֪a��bΪ��������a��0������f��x��=��ax+b+axlnx��f��e��=2��e=2.71828������Ȼ�����ĵ�������
��I����ʵ��b��ֵ��
��II������f��x���ĵ������䣻
��III����a=1ʱ���Ƿ�ͬʱ����ʵ��m��M��m��M����ʹ�ö�ÿһ��t��[m��M]��ֱ��y=t������y=f��x����x��[![]() ��e]�����й����㣿�����ڣ������С��ʵ��m������ʵ��M���������ڣ�˵�����ɣ�
��e]�����й����㣿�����ڣ������С��ʵ��m������ʵ��M���������ڣ�˵�����ɣ�
���𰸡���I��b=2
��II����a��0ʱ������f��x���ĵ�����������Ϊ��1��+�����������ݼ�����Ϊ��0��1����
��a��0ʱ������f��x���ĵ�����������Ϊ��0��1���������ݼ�����Ϊ��1��+������
��III��������
��������
���⣨I����x=e���뺯��f��x��=��ax+b+axlnx���ⷽ�̼������ʵ��b��ֵ��
��II�������жϵ����ķ��ţ�ȷ�������ĵ������䣻
��III���������ʵ��m��M��m��M����ʹ�ö�ÿһ��t��[m��M]��ֱ��y=t������y=f��x����x��[![]() ��e]�����й����㣬ת��Ϊ���õ�������y=f��x��������[
��e]�����й����㣬ת��Ϊ���õ�������y=f��x��������[![]() ��e]�ϵ�ֵ��
��e]�ϵ�ֵ��
�⣺��I����f��e��=2������f��x��=��ax+b+axlnx��
��b=2��
��II���ɣ�I���ɵ�f��x��=��ax+2+axlnx������f��x���Ķ�����Ϊ��0��+������
�Ӷ�f����x��=alnx��
��a��0����
����a��0ʱ����f����x����0��x��1����f����x����0��0��x��1��
����a��0ʱ����f����x����0��0��x��1����f����x����0��x��1��
���ϣ���a��0ʱ������f��x���ĵ�����������Ϊ��1��+�����������ݼ�����Ϊ��0��1����
��a��0ʱ������f��x���ĵ�����������Ϊ��0��1���������ݼ�����Ϊ��1��+������
��III����a=1ʱ��f��x��=��x+2+xlnx��f����x��=lnx��
�ɣ�II���ɵã���x����![]() ��e����f��x����f����x���仯������±���
��e����f��x����f����x���仯������±���
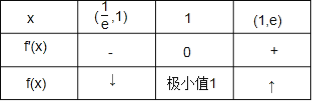
��f��![]() ��=2��
��=2��![]() ��2��
��2��
����y=f��x����[![]() ��e]�ϵ�ֵ��Ϊ[1��2]��
��e]�ϵ�ֵ��Ϊ[1��2]��
�ݴ˿ɵã���![]() �����ÿһ��t��[m��M]��ֱ��y=t������y=f��x����x��[
�����ÿһ��t��[m��M]��ֱ��y=t������y=f��x����x��[![]() ��e]�����й����㣻
��e]�����й����㣻
���Ҷ�ÿһ��t����������m������M��+������ֱ��y=t������y=f��x����x��[![]() ��e]����û�й����㣻
��e]����û�й����㣻
���ϵ�a=1ʱ��������Сʵ��m=1������ʵ��M=2��m��M����ʹ�ö�ÿһ��t��[m��M]��ֱ��y=t������y=f��x����x��[![]() ��e]�����й����㣮
��e]�����й����㣮

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�