题目内容
【题目】已知向量 ![]() =(m,﹣1),
=(m,﹣1), ![]() =(
=( ![]() )
)
(1)若m=﹣ ![]() ,求
,求 ![]() 与
与 ![]() 的夹角θ;
的夹角θ;
(2)设 ![]() . ①求实数m的值;
. ①求实数m的值;
②若存在非零实数k,t,使得[ ![]() +(t2﹣3)
+(t2﹣3) ![]() ]⊥(﹣k
]⊥(﹣k ![]() +t
+t ![]() ),求
),求 ![]() 的最小值.
的最小值.
【答案】
(1)解:向量 ![]() =(m,﹣1),
=(m,﹣1), ![]() =(
=( ![]() ),若m=﹣
),若m=﹣ ![]() ,
, ![]() 与
与 ![]() 的夹角θ,
的夹角θ,
则有cosθ= ![]() =
= 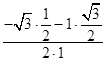 =﹣
=﹣ ![]() ,∴θ=
,∴θ= ![]()
(2)解:①设 ![]() ,则
,则 ![]() =
= ![]() ﹣
﹣ ![]() =0,∴m=
=0,∴m= ![]() .
.
②由①可得, ![]() =(
=( ![]() ,﹣1),
,﹣1), ![]() =
= ![]() ﹣
﹣ ![]() =0,
=0,
若存在非零实数k,t,使得[ ![]() +(t2﹣3)
+(t2﹣3) ![]() ]⊥(﹣k
]⊥(﹣k ![]() +t
+t ![]() ),故有[
),故有[ ![]() +(t2﹣3)
+(t2﹣3) ![]() ](﹣k
](﹣k ![]() +t
+t ![]() )=0,
)=0,
∴﹣k ![]() +[﹣k(t2﹣3)+t]
+[﹣k(t2﹣3)+t] ![]() +t(t2﹣3)
+t(t2﹣3) ![]() =﹣k4+0+t(t2﹣3)=0,∴4k=t(t2﹣3),
=﹣k4+0+t(t2﹣3)=0,∴4k=t(t2﹣3),
∴ ![]() =
= ![]() +t=
+t= ![]() =
= ![]() ≥﹣
≥﹣ ![]() ,当且仅当t=﹣2时,取等号,
,当且仅当t=﹣2时,取等号,
故 ![]() 的最小值为﹣
的最小值为﹣ ![]() .
.
【解析】(1)由条件利用两个向量的数量积的定义求得cosθ= 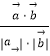 的值,可得θ的值.(2)①利用两个向量垂直的性质,求得m的值.②根据[
的值,可得θ的值.(2)①利用两个向量垂直的性质,求得m的值.②根据[ ![]() +(t2﹣3)
+(t2﹣3) ![]() ](﹣k
](﹣k ![]() +t
+t ![]() )=0,求得4k=t(t2﹣3),从而求得
)=0,求得4k=t(t2﹣3),从而求得 ![]() =
= ![]() ,再利用二次函数的性质求得它的最小值.
,再利用二次函数的性质求得它的最小值.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目