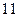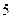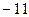题目内容
(本题满分12分)已知数列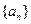 ,
,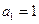 ,
,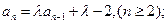
(Ⅰ)当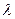 为何值时,数列
为何值时,数列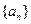 可以构成公差不
可以构成公差不 为零的等差数列,并求其通项公式;
为零的等差数列,并求其通项公式;
(Ⅱ)若 ,令
,令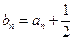 ,求数列
,求数列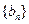 的前
的前 项和
项和 。
。
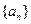 ,
,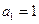 ,
,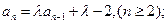
(Ⅰ)当
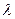 为何值时,数列
为何值时,数列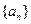 可以构成公差不
可以构成公差不 为零的等差数列,并求其通项公式;
为零的等差数列,并求其通项公式;(Ⅱ)若
 ,令
,令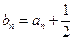 ,求数列
,求数列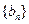 的前
的前 项和
项和 。
。(Ⅰ)
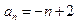
(Ⅱ)
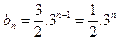
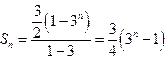
解: 1)
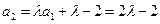
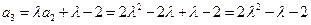 --------1分
--------1分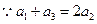
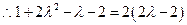
得
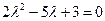
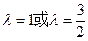 -----------------3分
-----------------3分当
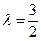 时,
时, 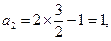
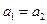 不合题意舍去-----------4分
不合题意舍去-----------4分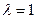 时,带入
时,带入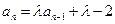 可得:
可得: 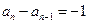 ---------------------------5分
---------------------------5分 构成以
构成以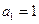 为首项,公差为 -1 的等差数列;
为首项,公差为 -1 的等差数列;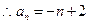 ------------ ----6分
------------ ----6分2)由
 可得,
可得,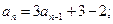
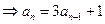 ,
,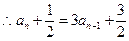
就有
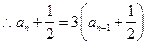 ,-------------------------------------------------.8分
,-------------------------------------------------.8分即
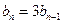 ,
,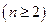 ,又
,又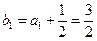
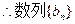 构成以
构成以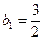 为首项,公比为3 的等比数
为首项,公比为3 的等比数 列;
列;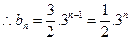 ----------10分
----------10分 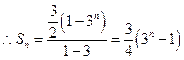 -----------12分
-----------12分(若由
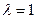 时,直接得:
时,直接得: 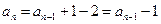 ;即
;即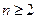 时,
时,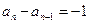 恒成立,
恒成立, 构成以
构成以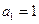 为首项,公差为1 的等差数列; 高#考#资#
为首项,公差为1 的等差数列; 高#考#资#则
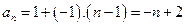 .………该解法不严谨本小题扣2分)
.………该解法不严谨本小题扣2分)
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 的前
的前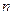 项和为
项和为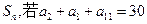 ,那么
,那么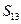 值的是 ( )
值的是 ( )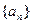 满足
满足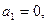
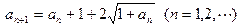 ,则
,则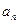 =___ .
=___ .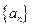 是等差数列,且
是等差数列,且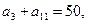 又
又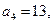 则
则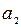 =" " ( )
=" " ( )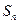 等差数列
等差数列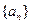 的前n项和,若
的前n项和,若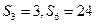 ,则
,则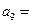 ________________.
________________.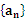 的前n项和为Sn,已知a15,且nSn+12n(n+1)+(n+1)Sn(
的前n项和为Sn,已知a15,且nSn+12n(n+1)+(n+1)Sn(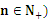 ,则与过点P(n,an)和点Q(n+2,an+1) (
,则与过点P(n,an)和点Q(n+2,an+1) ( , 2)
, 2) 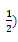
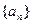 是公差为d的等差数列,其前n项和为Sn,则有
是公差为d的等差数列,其前n项和为Sn,则有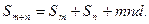 类似的,对于公比为q的等比数列
类似的,对于公比为q的等比数列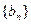 来说,设其前n项积为Tn,则关于
来说,设其前n项积为Tn,则关于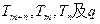 的一个关系式为 。
的一个关系式为 。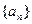 的前n项和
的前n项和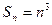 则
则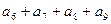 等于( )
等于( )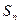 为等比数列
为等比数列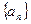 的前n项和,
的前n项和, ,则
,则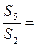 ( )
( )