题目内容
(本题满分14分)设
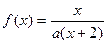 ,方程
,方程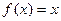 有唯一解,已知
有唯一解,已知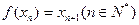 ,且
,且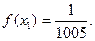
(1)求数列
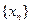 的通项公式;
的通项公式;(2)若
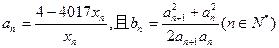 ,求和
,求和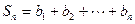 ;
;(3)问:是否存在最小整数
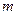 ,使得对任意
,使得对任意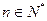 ,有
,有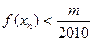 成立,若存在;求出
成立,若存在;求出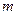 的值;若不存在,说明理由。
的值;若不存在,说明理由。 ,
,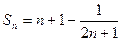 ,存在最小的正整数
,存在最小的正整数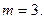
解:(1)因为方程
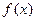
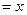 有唯一解,可求
有唯一解,可求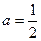 从而得到
从而得到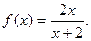
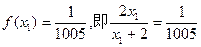
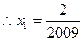 ,
,又由已知
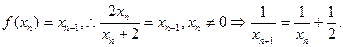
数列
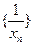 是首项为
是首项为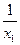 ,公差为
,公差为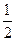 的等差数列 4分
的等差数列 4分故
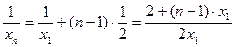 ,
,所以数列
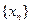 的通项公式为
的通项公式为 6分
6分(2)将
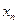 代入
代入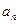 可求得
可求得
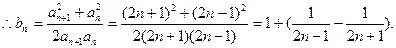
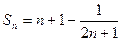 10分
10分(3)
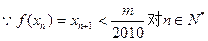 恒成立,
恒成立, 只要
只要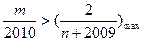 即可,
即可,而
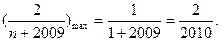 12分
12分即要
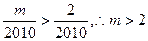 ,故存在最小的正整数
,故存在最小的正整数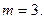 14分
14分
练习册系列答案
相关题目
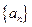 的前n项积为
的前n项积为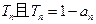 ;数列
;数列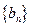 的前n项和为
的前n项和为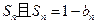 .
.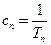 .①证明数列
.①证明数列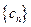 成等差数列;②求证数列
成等差数列;②求证数列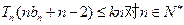 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.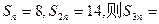 .
.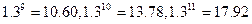 )
)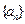 的首项
的首项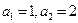 ,前
,前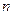 项和
项和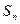 恒为正数,且当
恒为正数,且当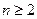 时,
时,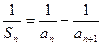 .
.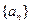 的通项公式;
的通项公式;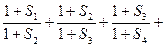
 .
.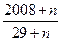 与
与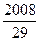 之间所有正整数的和不小于2008,则n的最小值为 .
之间所有正整数的和不小于2008,则n的最小值为 . 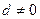 的等差数列{an}中的项组成一个新数列
的等差数列{an}中的项组成一个新数列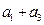 ,
, 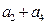 ,
,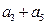 ,…,则下列说法正确的是
,…,则下列说法正确的是 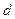 的等差数列
的等差数列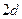 的等差数列
的等差数列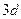 的等差数列
的等差数列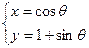 的中心到直线y=kx的距离记为d=f(k)给出下列判断
的中心到直线y=kx的距离记为d=f(k)给出下列判断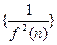 的前n项和是
的前n项和是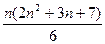
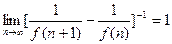 ④
④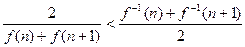
 中,
中, ,则
,则 的值为
的值为