题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)求函数![]() 在区间
在区间![]() 上的最大值
上的最大值![]() .
.
【答案】(1)见解析(2)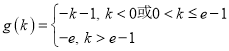
【解析】
(1)首先求出函数的导函数,令![]() 解得
解得![]() ,再对
,再对![]() 分类讨论即可得解;
分类讨论即可得解;
(2)对![]() 分类讨论,结合(1)中的结论,计算可得;
分类讨论,结合(1)中的结论,计算可得;
解:(1)因为![]() ,所以
,所以![]() ,
,
由![]() 解得
解得![]() .
.
①当![]() 时,
时,
|
|
|
|
| - | 0 | + |
|
| 极小值 |
|
所以,当![]() 时,
时,![]() 有极小值
有极小值![]() ;
;
②当![]() 时,
时,
|
|
|
|
| + | 0 | - |
|
| 极大值 |
|
所以,当![]() 时,
时,![]() 有极大值
有极大值![]() ;
;
综上,当![]() 时,当
时,当![]() 时,
时,![]() 有极小值
有极小值![]() ;
;
当![]() 时,当
时,当![]() 时,
时,![]() 有极大值
有极大值![]() .
.
(2)当![]() 时,由(1)知,
时,由(1)知,![]() 为
为![]() 上单调减函数,而
上单调减函数,而![]() ,
,
所以,![]() 为
为![]() 上单调减函数,故
上单调减函数,故![]() 的最大值
的最大值![]() ;
;
当![]() 时,
时,![]() ,由(1)知,
,由(1)知,![]() 为
为![]() 上单调减函数,而
上单调减函数,而![]() ,
,
所以,![]() 为
为![]() 上单调减函数,故
上单调减函数,故![]() 的最大值
的最大值![]() ;
;
当![]() 时,由(1)知,
时,由(1)知,![]() 为
为![]() 上单调减函数,
上单调减函数,![]() 上单调增函数,
上单调增函数,
又满足![]() ,故
,故![]() 的最大值
的最大值![]() ;
;
当![]() 时,由(1)知,
时,由(1)知,![]() 为
为![]() 上单调减函数,
上单调减函数,![]() 上单调增函数,
上单调增函数,
又满足![]() ,故
,故![]() 的最大值
的最大值![]() ;
;
综上,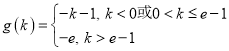 .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目