题目内容
【题目】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中，由四个全等的直角三角形和一个正方形构成．现有五种不同的颜色可供涂色，要求相邻的区域不能用同一种颜色，则不同的涂色方案有（ ）
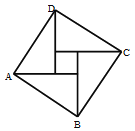
A.180B.192C.420D.480
【答案】C
【解析】
就使用颜色的种类分类计数可得不同的涂色方案的总数.
相邻的区域不能用同一种颜色，则涂5块区域至少需要3种颜色.
若5块区域只用3种颜色涂色，则颜色的选法有
，相对的两个直角三角形必同色，此时共有不同的涂色方案数为
（种）.
若5块区域只用4种颜色涂色，则颜色的选法有
，相对的两个直角三角形必同色，余下两个直角三角形不同色，此时共有不同的涂色方案数为
（种）.
若5块区域只用5种颜色涂色，则每块区域涂色均不同，此时共有不同的涂色方案数为
（种）.
综上，共有不同的涂色方案数为
（种）.
故选：C.
练习册系列答案
相关题目
