题目内容
已知函数f(x)=2 .
.
(1)求证:f(x)≤5,并说明等号成立的条件;
(2)若关于x的不等式f(x)≤|m-2|恒成立,求实数m的取值范围.
 .
.(1)求证:f(x)≤5,并说明等号成立的条件;
(2)若关于x的不等式f(x)≤|m-2|恒成立,求实数m的取值范围.
(1)见解析,x=4时,等号成立(2)(-∞,-3]∪[7,+∞)
(1)证明:由柯西不等式得(2 )2≤(22+12)[(
)2≤(22+12)[( )2+(
)2+( )2]=25.
)2]=25.
所以f(x)=2 ≤5.
≤5.
当且仅当 ,即x=4时,等号成立.
,即x=4时,等号成立.
(2)由(1)知f(x)≤5,又不等式f(x)≤|m-2|恒成立,
所以|m-2|≥5,解得m≥7或m≤-3.
故m的取值范围为(-∞,-3]∪[7,+∞)
 )2≤(22+12)[(
)2≤(22+12)[( )2+(
)2+( )2]=25.
)2]=25.所以f(x)=2
 ≤5.
≤5.当且仅当
 ,即x=4时,等号成立.
,即x=4时,等号成立.(2)由(1)知f(x)≤5,又不等式f(x)≤|m-2|恒成立,
所以|m-2|≥5,解得m≥7或m≤-3.
故m的取值范围为(-∞,-3]∪[7,+∞)

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 ≤a2+b2+c2<1.
≤a2+b2+c2<1. +
+ +
+ 的最小值.
的最小值. 、
、 是不全为零的实数,试比较
是不全为零的实数,试比较 与
与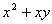 的大小;
的大小; 为正数,且
为正数,且 ,求证:
,求证: .
. 的解集为 .
的解集为 .