题目内容
【题目】已知函数![]() 是
是![]() 上的偶函数,对于
上的偶函数,对于![]() 都有
都有![]() 成立,且
成立,且![]() ,当
,当![]() ,
,![]() ,且
,且![]() 时,都有
时,都有![]() .则给出下列命题:①
.则给出下列命题:①![]() ;②
;②![]() 为函数
为函数![]() 图象的一条对称轴;③函数
图象的一条对称轴;③函数![]() 在
在![]() 上为减函数;④方程
上为减函数;④方程![]() 在
在![]() 上有4个根;其中正确的命题个数为( )
上有4个根;其中正确的命题个数为( )
A.1B.2C.3D.4
【答案】D
【解析】
由![]() 可得
可得![]() ,结合偶函数的性质可得
,结合偶函数的性质可得![]() ,从而推出
,从而推出![]() ,可得函数
,可得函数![]() 是以6为周期的周期函数,从而可判断①②,又根据当
是以6为周期的周期函数,从而可判断①②,又根据当![]() ,
,![]() ,且
,且![]() 时,都有
时,都有![]() 可得函数在
可得函数在![]() 上单调递增,结合函数值以及对称性可判断③④.
上单调递增,结合函数值以及对称性可判断③④.
解:对于①,令![]() ,由
,由![]() 得
得![]() ,
,
又函数![]() 是
是![]() 上的偶函数,
上的偶函数,
∴![]() ,
,
∴![]() ,
,
即函数![]() 是以6为周期的周期函数,
是以6为周期的周期函数,
∴![]() ;
;
又![]() ,所以
,所以![]() ,从而
,从而![]() ,即①正确;
,即①正确;
对于②,函数关于y轴对称,周期为6,
∴函数![]() 图象的一条对称轴为
图象的一条对称轴为![]() ,故②正确;
,故②正确;
对于③,当![]() ,
,![]() ,且
,且![]() 时,都有
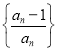
时,都有![]() ,设
,设![]() ,
,
则![]() ,故函数
,故函数![]() 在
在![]() 上是增函数,
上是增函数,
根据对称性,易知函数![]() 在
在![]() 上是减函数,
上是减函数,
根据周期性,函数![]() 在
在![]() 上为减函数,故③正确;
上为减函数,故③正确;
对于④,因为![]() ,又由其单调性及周期性可知
,又由其单调性及周期性可知
在![]() ,有且仅有
,有且仅有![]() ,
,
即方程![]() 在
在![]() 上有4个根,故④正确;
上有4个根,故④正确;
故选:D.

练习册系列答案
相关题目