Question

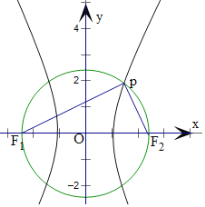
【题目】双曲线C：1（a＞0，b＞0）的左右焦点为F1，F2（|F1F2|＝2c），以坐标原点O为圆心，以c为半径作圆A，圆A与双曲线C的一个交点为P，若三角形F1PF2的面积为a2，则C的离心率为_____．

Answer 1

【答案】

【解析】

不妨设为右支上一点，设，运用双曲线的定义和直径所对的圆周角为直角，结合勾股定理和三角形的面积公式，可得的关系式，即可求解双曲线的离心率，得到答案.

不妨设P为右支上一点，设|PF1|＝m，|PF2|＝n，

由双曲线的定义可得m﹣n＝2a，

由题意可得△PF1F2为直角三角形，且∠F1PF2＝90°，

可得m2+n2＝4c2，且mn＝a2，

由（m﹣n）2＝m2+n2﹣2mn＝4c2﹣4a2＝4a2，即为ca，

可得e.

故答案为：.