Question

7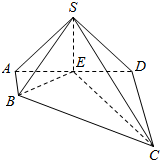．如图，在四棱锥S-ABCD中，AB⊥AD，AB∥CD，CD=3AB=3，平面SAD⊥平面ABCD，E是线段AD上一点，AE=ED=$\sqrt{3}$，SE⊥AD．
（1）写出一个平面，使它与平面SEC垂直；
（2）若SE=1，求三棱锥E-SBC的体积．

Answer 1

分析 （1）由平面SAD⊥平面ABCD，知SE⊥平面ABCD，所以SE⊥BE，由四边形ABCD是直角梯形，AB∥CD，AE=AB，DE=DC，知△EAB，△EDC都是等腰直角三角形，所以BE⊥CE，由此能够证明平面SBE⊥平面SEC．
（2）由题设条件求出S_△SBC，即可求出V_S-CBE．

解答 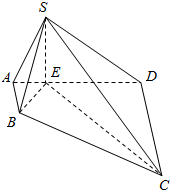（1）解：平面SBE⊥平面SEC．
证明：∵平面SAD⊥平面ABCD，平面SAD∩平面ABCD=AD，SE?平面SAD，SE⊥AD
∴SE⊥平面ABCD，（1分）
∵BE?平面ABCD，∴SE⊥BE．（2分）
∵四边形ABCD是直角梯形，AB∥CD，AE=$\sqrt{3}$AB=$\sqrt{3}$，DC=$\sqrt{3}$DE=3，
∴△EAB∽△EDC，
∴∠AEB+∠CEF=90°，∠BEC=90°，BE⊥CE．（4分）
∵SE?平面SEC，CE?平面SEC，SE∩CE=E，
∴BE⊥平面SEC，
∵BE?平面SBE，∴平面SBE⊥平面SEC．
（2）解：∵AB⊥AD，AB∥CD，CD=3AB=3，AE=ED=$\sqrt{3}$，SE⊥AD，
∴BE=2，CE=$\sqrt{9+3}$=2$\sqrt{3}$，SB=$\sqrt{5}$，SC=$\sqrt{12+1}$=$\sqrt{13}$，BC=$\sqrt{（2\sqrt{3}）^{2}+（3-1）^{2}}$=4，
∴cos∠SBC=$\frac{5+16-13}{2\sqrt{5}•4}$=$\frac{\sqrt{5}}{5}$，
∴sin∠SBC=$\frac{2\sqrt{5}}{5}$，
∴S_△SBC=$\frac{1}{2}×\sqrt{5}×4×\frac{2\sqrt{5}}{5}$=4，（8分）
∵SE=1，∴V_S-CBE=$\frac{1}{3}×\frac{1}{2}×BE×CE×SE$=$\frac{1}{3}×\frac{1}{2}×2×2\sqrt{3}×1$=$\frac{2\sqrt{3}}{3}$．（10分）

点评 本题综合考查了面面垂直的性质定理，线面垂直的判定定理，线面垂直的性质定理以及棱锥的体积公式等，涉及到的知识较多，综合性很强．