题目内容
【题目】已知数列![]() 满足
满足![]() (
(![]() ),
),![]() (
(![]() ).
).
(1)若![]() ,证明:
,证明:![]() 是等比数列;
是等比数列;
(2)若存在![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
① 求数列![]() 的通项公式;
的通项公式;
② 证明:![]() .
.
【答案】(1)见解析;(2)①![]() ,②见解析
,②见解析
【解析】
(1)对![]() 两边同除以
两边同除以![]() 并整理得:
并整理得:![]() ,结合
,结合![]() 即可证得
即可证得![]() 是等比数列,问题得证。
是等比数列,问题得证。
(2)①设![]() ,由(1)可得
,由(1)可得![]() ,结合
,结合![]() ,
,![]() ,
,![]() 成等差数列即可求得
成等差数列即可求得![]() ,问题得解。
,问题得解。
②将![]() 转化成
转化成![]() ,令
,令![]() ,且
,且![]() ,即可再转化成
,即可再转化成![]() ,记
,记![]() (
(![]() ),利用导数即可求得
),利用导数即可求得![]() ,问题得证。
,问题得证。
(1)由![]() ,得
,得![]() ,得
,得![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() (
(![]() ),
),
所以![]() 是以
是以![]() 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
(2)① 设![]() ,由(1)知,
,由(1)知,![]() , 所以
, 所以![]() ,即
,即![]() ,
,
所以![]() .因为
.因为![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
则![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() .
.
② 要证![]() ,
,
即证![]() ,即证
,即证![]() .
.
设![]() ,则
,则![]() ,且
,且![]() ,
,
从而只需证,当![]() 时,
时,![]() . 设
. 设![]() (
(![]() ),
),
则![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
所以,原不等式得证.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某大学生参加社会实践活动,对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根据1至5月份的数据,先求出![]() 关于
关于![]() 的回归直线方程;6月份的数据作为检验数据.若由回归直线方程得到的预测数据与检验数据的误差不超过
的回归直线方程;6月份的数据作为检验数据.若由回归直线方程得到的预测数据与检验数据的误差不超过![]() ,则认为所得到的回归直线方程是理想的.试问所求得的回归直线方程是否理想?
,则认为所得到的回归直线方程是理想的.试问所求得的回归直线方程是否理想?
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的回归关系,如果该种机器配件的成本是![]() 元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考数据:![]() ,
,![]() .
.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: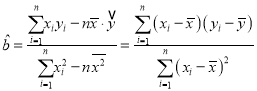 ,
,![]() .
.