题目内容
已知函数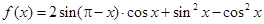 ,
,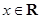 .
.
(1)求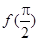 的值及函数
的值及函数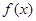 的最小正周期;
的最小正周期;
(2)求函数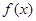 在
在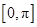 上的单调减区间.
上的单调减区间.
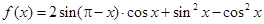 ,
,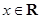 .
.(1)求
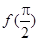 的值及函数
的值及函数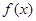 的最小正周期;
的最小正周期;(2)求函数
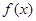 在
在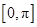 上的单调减区间.
上的单调减区间.(1)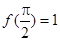 ,函数
,函数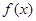 的最小正周期为
的最小正周期为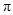 ;(2)函数
;(2)函数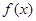 在
在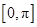 上的单调减区间为
上的单调减区间为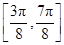 .
.
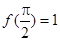 ,函数
,函数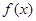 的最小正周期为
的最小正周期为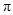 ;(2)函数
;(2)函数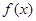 在
在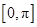 上的单调减区间为
上的单调减区间为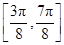 .
.试题分析:(1)求
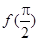 的值及函数
的值及函数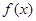 的最小正周期,首先对函数
的最小正周期,首先对函数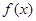 进行化简,将他化为一个角的一个三角函数,由已知
进行化简,将他化为一个角的一个三角函数,由已知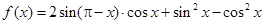 ,可用诱导公式及二倍角公式将函数
,可用诱导公式及二倍角公式将函数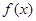 化为
化为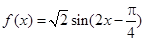 ,即可求出
,即可求出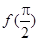 的值及函数
的值及函数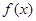 的最小正周期;(2)求函数
的最小正周期;(2)求函数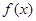 在
在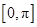 上的单调减区间,由(1)知
上的单调减区间,由(1)知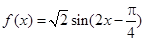 ,可利用
,可利用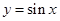 的单调递减区间得,
的单调递减区间得,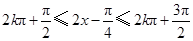 ,
,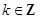 ,解出
,解出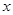 ,即得
,即得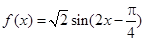 的单调递减区间得,从而得函数
的单调递减区间得,从而得函数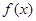 在
在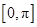 上的单调减区间.
上的单调减区间.试题解析:
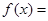
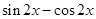
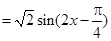 .
.(1)
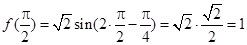 .
.显然,函数
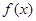 的最小正周期为
的最小正周期为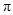 . 8分
. 8分(2)令
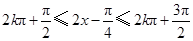 得
得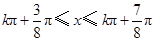 ,
,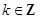 .
.又因为
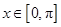 ,所以
,所以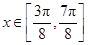 .
.函数
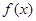 在
在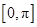 上的单调减区间为
上的单调减区间为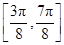 . 13分
. 13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
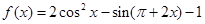 .
.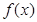 的最小正周期;
的最小正周期;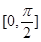 上的最小值和最大值.
上的最小值和最大值.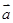 =
=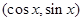 ,
,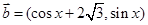 ,
,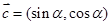 ,
,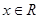 ,
,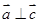 ,求
,求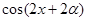 的值;(2)若
的值;(2)若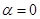 ,求函数
,求函数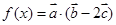 的最大值,并求出相应的
的最大值,并求出相应的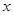 值.
值. 。
。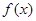 的单调递减区间;
的单调递减区间;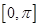 上的最大值及最小值;
上的最大值及最小值;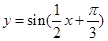 的图象作怎样的变换可得到
的图象作怎样的变换可得到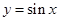 的图象?
的图象? 的图象,只需将
的图象,只需将 的图象()
的图象() 个单位长度
个单位长度 个单位长度
个单位长度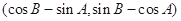 在( )
在( )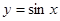 关于直线
关于直线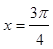 对称的曲线是( )
对称的曲线是( )


 在
在 上有两个零点,则
上有两个零点,则 的取值范围是( )
的取值范围是( )



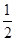 cos4x.
cos4x.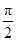 ,π),且f(α)=
,π),且f(α)=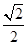 ,求α的值.
,求α的值.