题目内容
已知函数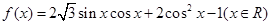 ,
,
(1)求函数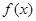 的最小正周期及在区间
的最小正周期及在区间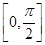 上的最大值和最小值;
上的最大值和最小值;
(2)若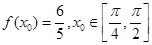 ,求
,求 的值.
的值.
(1)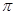 ,最大值为2,最小值为-1;(2)
,最大值为2,最小值为-1;(2)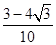 .
.
解析试题分析:(1)本小题中的函数是常考的一种形式,先用降幂公式与二倍角的正弦公式,再用辅助角公式化函数为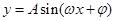 形式,此时用周期公式即可求得其周期,求
形式,此时用周期公式即可求得其周期,求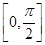 的最值可结合图像分析,也可用换元法先求出
的最值可结合图像分析,也可用换元法先求出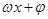 的范围,再用正弦函数图像分析这个范围的最值情况;(2)本小题中可先求出
的范围,再用正弦函数图像分析这个范围的最值情况;(2)本小题中可先求出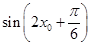 的值,结合
的值,结合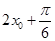 的范围求出
的范围求出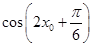 的值,而
的值,而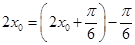 ,运用两角差的余弦公式,即可求出
,运用两角差的余弦公式,即可求出 的值.
的值.
试题解析:(1)解:由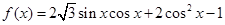 ,得
,得 ,所以函数
,所以函数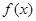 的最小正周期为
的最小正周期为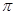 ,因为
,因为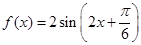 在区间
在区间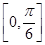 上为增函数,在区间
上为增函数,在区间 上为减函数,又
上为减函数,又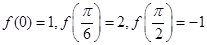 ,所以函数
,所以函数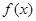 在区间
在区间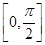 上的最大值为2,最小值为-1;
上的最大值为2,最小值为-1;
(2)由(1)可知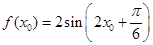 ,又因为
,又因为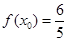 ,所以
,所以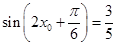 ,由
,由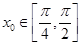 ,得
,得 ,从而
,从而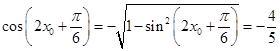 ,所以
,所以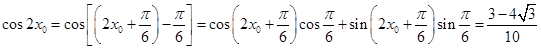 .
.
考点:降幂公式,二倍角的正弦公式,辅助角公式,周期公式,正弦函数图像,两角差的余弦公式,角的变换,化归思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
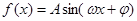

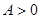 ,
,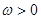 ,
,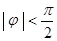
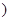
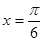 时,
时, 有最大值为
有最大值为 ,当
,当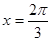 时,
时, .
. 表达式;(2)若
表达式;(2)若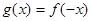 ,求
,求 的单调递减区间.
的单调递减区间. 的一系列对应值如下表:
的一系列对应值如下表:










 的一个解析式;
的一个解析式; 周期为
周期为 ,当
,当 时,
时, 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.  ,面积
,面积 ,求这个扇形的半径
,求这个扇形的半径 和圆心角
和圆心角 的弧度数.
的弧度数.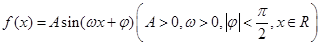 图象的一部分如图所示.
图象的一部分如图所示. 的解析式;
的解析式; 时,求函数
时,求函数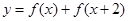 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.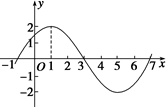
 ,函数
,函数 ,且
,且 的图像过点
的图像过点 和点
和点 .
. 的值;
的值; 个单位后得到函数
个单位后得到函数 的图像,若
的图像,若 的距离的最小值为1,求
的距离的最小值为1,求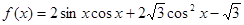 ,
,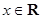 .
. 的最小正周期和单调递减区间;
的最小正周期和单调递减区间; 中的三个内角
中的三个内角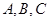 所对的边分别为
所对的边分别为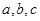 ,若锐角
,若锐角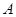 满足
满足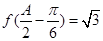 ,且
,且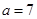 ,
,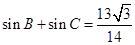 ,求
,求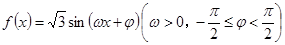 的图像关于直线
的图像关于直线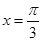 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为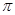 .
.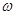 和
和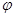 的值;
的值;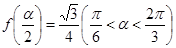 ,求
,求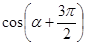 的值.
的值. ,则m= 。
,则m= 。