题目内容
已知动圆 与圆
与圆 相切,且与圆
相切,且与圆 相内切,记圆心
相内切,记圆心 的轨迹为曲线
的轨迹为曲线 ;设
;设 为曲线
为曲线 上的一个不在
上的一个不在 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点 作
作 的平行线交曲线
的平行线交曲线 于
于 两个不同的点.
两个不同的点.
(1)求曲线 的方程;
的方程;
(2)试探究 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(3)记 的面积为
的面积为 ,求
,求 的最大值.
的最大值.
(1)圆心 的轨迹
的轨迹 :
: ;
;
(2) 和
和 的比值为一个常数,这个常数为
的比值为一个常数,这个常数为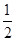 ;
;
(3)当 时,
时, 取最大值
取最大值 .
.
解析试题分析:(1)设圆心 的坐标为
的坐标为 ,半径为
,半径为
利用已知条件,判断得到动圆 与圆
与圆 只能内切,
只能内切,
从而由
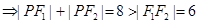 ,
,
判断得出圆心 的轨迹为以
的轨迹为以 为焦点的椭圆,且
为焦点的椭圆,且 ,
,
求得圆心 的轨迹
的轨迹 :
: ;
;
(2)设 ,研究直线
,研究直线 ,直线
,直线 与椭圆联立的方程组,应用韦达定理,弦长公式,确定
与椭圆联立的方程组,应用韦达定理,弦长公式,确定 作出结论;
作出结论;
(3)注意到 的面积
的面积 的面积,
的面积,
利用 到直线
到直线 的距离
的距离 ,将面积表示为
,将面积表示为 ,应用“换元”思想,
,应用“换元”思想,
令 ,得到
,得到 应用基本不等式得解.
应用基本不等式得解.
试题解析:(1)设圆心 的坐标为
的坐标为 ,半径为
,半径为
由于动圆 与圆
与圆 相切,且与圆
相切,且与圆 相内切,所以动
相内切,所以动
圆 与圆
与圆 只能内切
只能内切
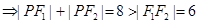 2分
2分 圆心
圆心 的轨迹为以
的轨迹为以 为焦点的椭圆,其中
为焦点的椭圆,其中 ,
,
故圆心 的轨迹
的轨迹 :
: 4分
4分
(2)设 ,直线
,直线 ,则直线
,则直线
由 可得:
可得: ,
, 
 6分
6分
由 可得:
可得:





 8分
8分


 和
和 的比值为一个常数,这个常数为
的比值为一个常数,这个常数为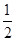 &nb
&nb

练习册系列答案
相关题目
 中,点
中,点 ,直线
,直线 .设圆
.设圆 的半径为
的半径为 ,圆心在
,圆心在 上.
上. 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心 的取值范围.
的取值范围.
 ,求圆C方程.
,求圆C方程.
 为何值时,曲线C表示圆;
为何值时,曲线C表示圆; 交于M、N两点,且
交于M、N两点,且 ,求
,求 与圆
与圆 交于
交于 ,
, 两点,是否存在实数
两点,是否存在实数 为直径的圆过原点,若存在,求出实数
为直径的圆过原点,若存在,求出实数
