题目内容
已知曲线C:
(1)当 为何值时,曲线C表示圆;
为何值时,曲线C表示圆;
(2)在(1)的条件下,若曲线C与直线 交于M、N两点,且
交于M、N两点,且 ,求
,求 的值.
的值.
(3)在(1)的条件下,设直线 与圆
与圆 交于
交于 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得以
,使得以 为直径的圆过原点,若存在,求出实数
为直径的圆过原点,若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) 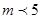 (2)
(2)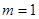 (3)存在,
(3)存在,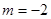
解析试题分析:
(1)根据圆的一般式可知, 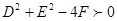 ,可得
,可得 范围;
范围;
(2)将(1)中圆变形为标准方程,可知 存在于半径中,所以根据圆中
存在于半径中,所以根据圆中 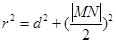 ,先求出圆心到直线的距离
,先求出圆心到直线的距离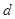 ,即可求半径得
,即可求半径得 .
.
(3)假设存在,则有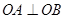 ,设出两点坐标,可得
,设出两点坐标,可得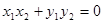 .根据直线与圆的位置关系是相交,所以联立后首先根据
.根据直线与圆的位置关系是相交,所以联立后首先根据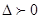 初步判断
初步判断 的范围,而后利用根与系数的关系用
的范围,而后利用根与系数的关系用 表示出
表示出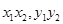 ,将其带入
,将其带入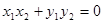 解之,如有解且在
解之,如有解且在 的范围内,则存在,否则不存在.
的范围内,则存在,否则不存在.
(1)由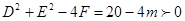 ,得
,得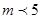 .
.
(2) ,即
,即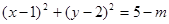 ,
,
所以圆心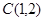 ,半径
,半径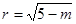 ,
,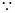 圆心
圆心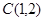 到直线
到直线 的距离
的距离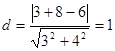 .
.
又 ,在圆中
,在圆中
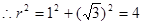 ,即
,即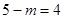 ,
,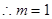 .
.
(3)假设存在实数 使得以
使得以 为直径的圆过原点,则
为直径的圆过原点,则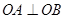 ,所以
,所以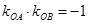 .
.
设 ,则有
,则有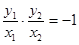 ,即
,即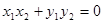 .
.
由 得
得 ,
,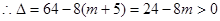 ,即
,即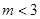 ,又由(1)知
,又由(1)知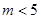 ,
,
故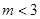
根据根与系数的关系知: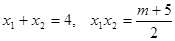
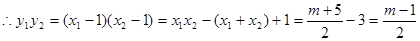 ,
,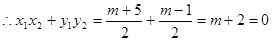
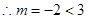
故存在实数 使得以
使得以 为直径的圆过原点,
为直径的圆过原点,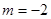
考点:圆的一般方程的判断,直线与圆的位置关系的应用, 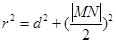 的使用.
的使用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. 有公共点的概率.
有公共点的概率. 上,求圆C的方程。
上,求圆C的方程。 与圆
与圆 相切,且与圆
相切,且与圆 相内切,记圆心
相内切,记圆心 ;设
;设 为曲线
为曲线 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点 作
作 的平行线交曲线
的平行线交曲线 两个不同的点.
两个不同的点. 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由; 的面积为
的面积为 ,求
,求 与已知圆
与已知圆 的交点,且在两坐标轴上的四个截距之和为8的圆的方程。
的交点,且在两坐标轴上的四个截距之和为8的圆的方程。 为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点. 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为 ,则四边形ABCD的面积的最大值为 .
,则四边形ABCD的面积的最大值为 .