题目内容
己知圆C:(x-xo)2+(y-y0)2=R2(R>0)与y轴相切,圆心C在直线l:x-3y=0上,且圆C截直线m:x-y=0所得的弦长为2 ,求圆C方程.
,求圆C方程.
(x-3)2+(y-1)2=9或(x+3)2+(y+1)2=9
解析试题分析:利用题中圆的方程,和已知条件,可知|x0|=R,又由于圆心在直线x-3y=0上可知x0=3y0,根据圆C截直线m:x-y=0所得的弦长为2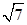 ,由勾股定理可知
,由勾股定理可知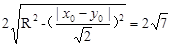 ,三方程联立即可求出结果.
,三方程联立即可求出结果.
解:圆C:(x-xo)2+(y-y0)2=R2(R>0)与y轴相切,则|x0|=R (1)
圆心C在直线l:x-3y=0上,则x0=3y0 (2)
圆C截直线m:x-y=0所得的弦长为2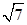 ,则
,则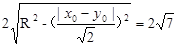
把(1)(2)代入上式消去x0,y0得:R=3,则x0=3,y0="1" 或x0=-3,y0=-1
故所求圆C的方程为:(x-3)2+(y-1)2=9或(x+3)2+(y+1)2=9
考点:1.圆的性质;2.直线与圆的位置关系.

练习册系列答案
相关题目
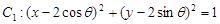 与圆
与圆 ,在下列说法中:
,在下列说法中: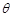 ,圆
,圆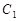 与圆
与圆 始终相切;
始终相切;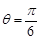 时,圆
时,圆 截得的弦长为
截得的弦长为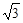 ;
;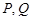 分别为圆
分别为圆 的最大值为4.
的最大值为4.
 (
( )
) 时,求经过原点且与圆
时,求经过原点且与圆 相切的直线
相切的直线 的方程;
的方程; 的内部,求实数
的内部,求实数 的取值范围.
的取值范围. ,动点P 满足:|PA|=2|PB|.
,动点P 满足:|PA|=2|PB|. ,求此曲线的方程;
,求此曲线的方程; 与圆
与圆 相切,且与圆
相切,且与圆 相内切,记圆心
相内切,记圆心 ;设
;设 为曲线
为曲线 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点 作
作 的平行线交曲线
的平行线交曲线 两个不同的点.
两个不同的点. 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由; 的面积为
的面积为 ,求
,求 的方程为:
的方程为: (
( ,
, 为常数).
为常数). 轴、
轴、 轴交于点
轴交于点 、
、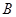 (
( ),试判断
),试判断 的面积
的面积 是否为定值?并证明你的判断;
是否为定值?并证明你的判断; 与曲线
与曲线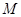 、
、 ,且
,且 ,求曲线
,求曲线 的方程:
的方程:
 相交于
相交于 ,
, 两点,且
两点,且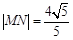 ,求
,求 的值
的值