题目内容
12.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,F为椭圆在x轴正半轴上的焦点,M,N两点在椭圆C上,且$\overrightarrow{MF}=λ\overrightarrow{FN}$(λ>0),定点A(-4,0),且$\overrightarrow{MN}⊥\overrightarrow{AF}$,$\overrightarrow{AM}•\overrightarrow{AN}=\frac{106}{3}$;(1)求椭圆C的方程;
(2)GH是过F点的弦,且当$\overrightarrow{AH}•\overrightarrow{AG}$×tan∠GAH的值为6$\sqrt{3}$,求出直线GH的方程.
分析 (1)依题意设M(c,t)、N(c,-t),则t2=$\frac{1}{3}$b2,代入$\frac{106}{3}$=$\overrightarrow{AM}$•$\overrightarrow{AN}$=(c+4,t)•(c+4,-t)化简可知c=2,进而可得结论;
(2)通过$\overrightarrow{AH}•\overrightarrow{AG}$×tan∠GAH=6$\sqrt{3}$及三角形面积公式化简可知(y1+y2)2-4y1y2=3,进而利用韦达定理计算可得结论.
解答 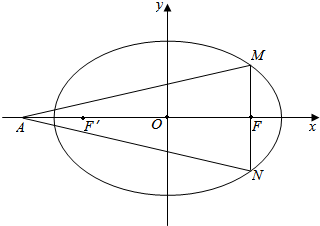 解:(1)依题意,MN⊥x轴,
解:(1)依题意,MN⊥x轴,
右焦点F(c,0),设M(c,t)、N(c,-t),则$\frac{{c}^{2}}{{a}^{2}}$+$\frac{{t}^{2}}{{b}^{2}}$=1,
∵椭圆离心率e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,即$\frac{{c}^{2}}{{a}^{2}}$=$\frac{2}{3}$,
∴$\frac{{t}^{2}}{{b}^{2}}$=$\frac{1}{3}$,t2=$\frac{1}{3}$b2,
∴$\frac{106}{3}$=$\overrightarrow{AM}$•$\overrightarrow{AN}$=(c+4,t)•(c+4,-t)
=c2+8c+16-$\frac{1}{3}$b2
=c2+8c+16-$\frac{1}{3}$(a2-c2)
=$\frac{4}{3}$c2+8c+16-$\frac{1}{3}$a2,
又∵$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,即a2=$\frac{3}{2}$c2,
∴上式可化为:$\frac{5}{6}$c2+8c-$\frac{58}{3}$=0,
解得:c=2,
∴a2=6,b2=2,
∴椭圆C的方程为:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1;
(2)由(1)知F(2,0),设直线GH的方程为:x=my+2,
联立$\left\{\begin{array}{l}{x=my+2}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,消去x、整理得:(m2+3)y2+4my-2=0,
设G(x1,y1)、H(x2,y2),则y1+y2=-$\frac{4m}{{m}^{2}+3}$,y1y2=-$\frac{2}{{m}^{2}+3}$,
∵$\overrightarrow{AH}•\overrightarrow{AG}$×tan∠GAH
=|$\overrightarrow{AH}$|•|$\overrightarrow{AG}$|sin∠GAH
=2S△GAH
=6$\sqrt{3}$,
∴S△GAH=2$\sqrt{3}$,
又∵S△GAH=$\frac{1}{2}$|AF|•|y1-y2|=3|y1-y2|,
∴|y1-y2|=$\sqrt{3}$,
∴(y1+y2)2-4y1y2=3,
即(-$\frac{4m}{{m}^{2}+3}$)2-4(-$\frac{2}{{m}^{2}+3}$)=3,
解得:m=±1,
∴直线GH的方程为:x-y-2=0或x+y-2=0.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 0 | B. | $-\frac{3}{2}$ | C. | 6 | D. | -2 |
| n | 1 | 2 | 3 | 4 | 5 | 6 |
| xn | 70 | 76 | 72 | 70 | 72 | x6 |
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{2}{3}$ | D. | -1 |