题目内容
棱长为1的正方体 被以A为球心,AB为半径的球相截,则所截得几何体(球内部分)的表面积为 ( )
被以A为球心,AB为半径的球相截,则所截得几何体(球内部分)的表面积为 ( )
 被以A为球心,AB为半径的球相截,则所截得几何体(球内部分)的表面积为 ( )
被以A为球心,AB为半径的球相截,则所截得几何体(球内部分)的表面积为 ( )A. | B.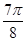 | C. | D. |
A
由题意可知截得的几何体占整个球体体积的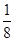 ,
,
所以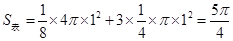 .
.
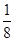 ,
,所以
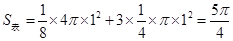 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 中,侧棱
中,侧棱 底面
底面 ,
, 为
为 的中点,
的中点, ,
, .
.
 平面
平面 ;
; 的体积.
的体积.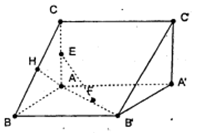
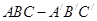 ,
,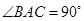 ,
,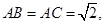 AA′=1,点M,N分别为
AA′=1,点M,N分别为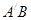 和
和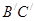 的中点。
的中点。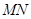 ∥平面
∥平面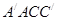 ;
; 的体积。(锥体体积公式V=
的体积。(锥体体积公式V=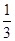 Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高)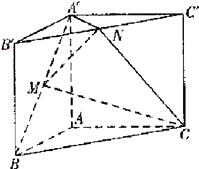
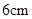 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.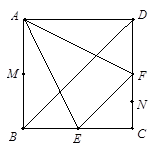
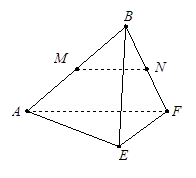
 中,侧面
中,侧面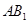 内有一动点
内有一动点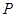 到直线
到直线 与直线
与直线 的距离相等,则动点
的距离相等,则动点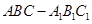 中,
中,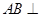 侧面
侧面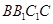 ,
,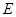 为棱
为棱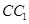 上异于
上异于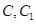 的一点,
的一点,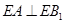 ,已知
,已知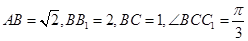 ,求:
,求: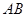 与
与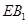 的距离;
的距离;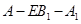 的平面角的正切值.
的平面角的正切值.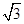 ,VC=7,画出二面角V-AB-C的平面角,并求它的余弦值。
,VC=7,画出二面角V-AB-C的平面角,并求它的余弦值。