题目内容
数列{an}的前n项和为Sn,已知Sn=
.
(1)求数列{an}的通项公式;
(2)若数列{cn}满足cn=
,求数列{cn}的前n项和为Tn.
| n2+3n |
| 2 |
(1)求数列{an}的通项公式;
(2)若数列{cn}满足cn=
|
(1)当n=1时,a1=s1=2
n≥2时,an=sn-sn-1=
-
=n+1
当n=1时,a1=2适合上式
故an=n+1
(2)当n为偶数时,Tn=(a1+a3+…+an-1)+(a2+a4+…+an)
=(2+4+…+n)+(22+24+…+2n)
=
+
=
+
当n为奇数时,n-1为偶数
Tn=(a1+a3+…+an)+(a2+a4+…+an-1)
=(2+4+…+n+1)+(22+24+…+2n-1)
=
+
=
+
∴Tn=
n≥2时,an=sn-sn-1=
| n2+3n |
| 2 |
| (n-1)2+3(n-1) |
| 2 |
当n=1时,a1=2适合上式
故an=n+1
(2)当n为偶数时,Tn=(a1+a3+…+an-1)+(a2+a4+…+an)
=(2+4+…+n)+(22+24+…+2n)
=
(2+n)•
| ||
| 2 |
4(1-4
| ||
| 1-4 |
=
| n(n+2) |
| 4 |
| 4(2n-1) |
| 3 |
当n为奇数时,n-1为偶数
Tn=(a1+a3+…+an)+(a2+a4+…+an-1)
=(2+4+…+n+1)+(22+24+…+2n-1)
=
(3+n)•
| ||
| 2 |
4(1-4
| ||
| 1-4 |
=
| n2+4n+3 |
| 4 |
| 4(2n-1-1) |
| 3 |
∴Tn=
|

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
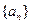 的公差
的公差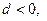 且
且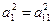 ,则数列
,则数列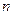 项和
项和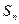 取得最大值时的项数
取得最大值时的项数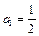 ,则
,则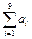 = .
= .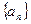 中,已知
中,已知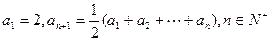 ,则
,则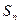 =______________
=______________