题目内容
已知数列{an}的通项公式an=-2n+11,前n项和Sn.
(1)求数列{an}的前n项和Sn;
(2)|a1|+|a2|+|a3|+…+|a14|.
(1)求数列{an}的前n项和Sn;
(2)|a1|+|a2|+|a3|+…+|a14|.
(1)∵an=-2n+11,
∴an+1-an=-2(n+1)+11-(-2n+11)=-2,
∴数列{an}为公差为2的等差数列,又a1=9,
∴数列{an}的前n项和Sn=
=
=10n-n2;
(2)由an=-2n+11≥0得:n≤
,又n∈N*,
∴当n=1,2,…5时,an>0,当n≥6时,an<0,
∴|a1|+|a2|+|a3|+…+|a14|
=a1+a2+…+a5-a6-a7-…-a14
=-a1-a2-…-a5-a6-a7-…-a14+2(a1+a2+…+a5)
=-
+2×
=-
+2×
=56+50
=106.
∴an+1-an=-2(n+1)+11-(-2n+11)=-2,
∴数列{an}为公差为2的等差数列,又a1=9,
∴数列{an}的前n项和Sn=
| (a1+an)×n |
| 2 |
| (9+11-2n)×n |
| 2 |
(2)由an=-2n+11≥0得:n≤
| 11 |
| 2 |
∴当n=1,2,…5时,an>0,当n≥6时,an<0,
∴|a1|+|a2|+|a3|+…+|a14|
=a1+a2+…+a5-a6-a7-…-a14
=-a1-a2-…-a5-a6-a7-…-a14+2(a1+a2+…+a5)
=-
| (a1+a14)×14 |
| 2 |
| (a1+a5)×5 |
| 2 |
=-
| (9-17)×14 |
| 2 |
| (9+1)×5 |
| 2 |
=56+50
=106.

练习册系列答案
相关题目
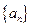 的前
的前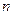 项和
项和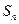 ,满足
,满足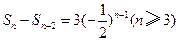 ,且
,且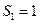 ,
,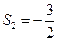 ,求数列
,求数列
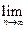
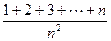 =( )
=( )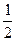 D 0
D 0