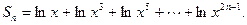题目内容
已知数列{an}了前n项和Sn=口n-1，则此数列了奇数项了前n项和是（ ）
A．
| B．
| C．
| D．
|
∵Sn=2n-0
∴S（n-0）=2（n-0）-0
∴an=Sn-S（n-0）=2（n-0） 而a0=0
∴an=2（n-0）
设奇数项组成数列{bn}
∴bn=22n-2∴{bn}是以0为首项，4为公比的等比数列．
∴Tn=
=
=
故选C．
∴S（n-0）=2（n-0）-0
∴an=Sn-S（n-0）=2（n-0） 而a0=0
∴an=2（n-0）
设奇数项组成数列{bn}
∴bn=22n-2∴{bn}是以0为首项，4为公比的等比数列．
∴Tn=
| b0(0-4n) |
| 0-4 |
| 4n-0 |
| 3 |
| 22n-0 |
| 3 |
故选C．
练习册系列答案
精英口算卡系列答案
相关题目
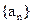满足：当n为奇数时，
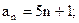当n为偶数时，
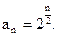则数列的前2m项的和（m是正整数）为 
