题目内容
如图所示,有三根针和套在一根针上的 个金属片,按下列规则,把金属片从一根针上全部移到另一根针上。
个金属片,按下列规则,把金属片从一根针上全部移到另一根针上。
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面。
若将 个金属片从1号针移到3号针最少需要移动的次数记为
个金属片从1号针移到3号针最少需要移动的次数记为 ,则
,则 =( )
=( )
| A.33 | B.31 | C.17 | D.15 |
B
解析试题分析:根据移动方法与规律发现,随着盘子数目的增多,都是分两个阶段移动,用盘子数目减1的移动次数都移动到2柱,然后把最大的盘子移动到3柱,再用同样的次数从2柱移动到3柱,从而完成,然后根据移动次数的数据找出总的规律求解即可.解:设h(n)是把n个盘子从1柱移到3柱过程中移动盘子之最少次数n=1时,h(1)=1; n=2时,小盘→2柱,大盘→3柱,小柱从2柱→3柱,完成,即h(2)=3=22-1; n=3时,小盘→3柱,中盘→2柱,小柱从3柱→2柱,[用h(2)种方法把中、小两盘移到2柱,大盘3柱;再用h(2)种方法把中、小两盘从2柱3柱,完成], h(3)=h(2)×h(2)+1=3×2+1=7=23-1, h(4)=h(3)×h(3)+1=7×2+1=15=24-1,…以此类推,h(n)=h(n-1)×h(n-1)+1=2n-1,故答案为31,故选B
考点:归纳推理
点评:本题考查了归纳推理、图形变化的规律问题,根据题目信息,得出移动次数分成两段计数是解题的关键.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案实验中学“数学王子”张小明在自习课上,对正整数1,2,3,4, 按如下形式排成数阵好朋友王大安问他“由上而下第20行中从左到右的第三个数是多少”张小明自上而下逐个排了两节课,终于找到了这个数,聪明的你一定知道这个数是( ) 
| A.190 | B.191 | C.192 | D.193 |
用反证法证明命题“三角形的内角中至少有一个角不大于 ”时,反设正确的是
”时,反设正确的是
A.假设三个内角都不大于 | B.假设三个内角都大于 |
C.假设三个内角至多有一个大于 | D.假设三个内角至多有二个大于 |
用反证法证明命题“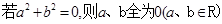 ”,其反设正确的是( )
”,其反设正确的是( )
A.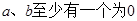 | B.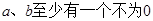 |
C.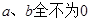 | D. |
在平面上,若两个正三角形的边长比为1:2.则它们的面积之比为1:4.类似地,在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为( )
| A.1:2 | B.1:4 | C.1:6 | D.1:8 |
观察式子: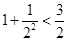 ,
,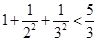 ,
,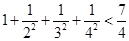 ,……则可归纳出式子(
,……则可归纳出式子(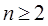 )( )
)( )
A. | B.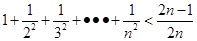 |
C.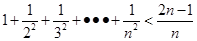 | D.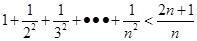 |
 )
)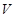 )
)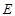 )
)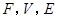 所满足的等式是_________.
所满足的等式是_________. 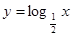 在
在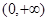 上是减函数”恢复成完全的三段论,其中大前提是 .
上是减函数”恢复成完全的三段论,其中大前提是 .