题目内容
将演绎推理：“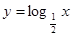
在
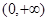上是减函数”恢复成完全的三段论，其中大前提是 ．
若
，则
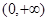在上是减函数
解析试题分析：由演绎推理的定义知：“
在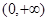上是减函数”，大前提为 若，则在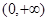上是减函数 .
考点：推理与证明.
练习册系列答案
相关题目
题目内容
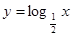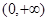将演绎推理：“在上是减函数”恢复成完全的三段论，其中大前提是 ．
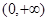若，则在上是减函数
解析试题分析：由演绎推理的定义知：“在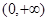上是减函数”，大前提为 若，则在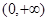上是减函数 .
考点：推理与证明.
个金属片，按下列规则，把金属片从一根针上全部移到另一根针上。
，则
=（ ）
＝
，则图(2)有体积关系：
＝________.
是椭圆
：
且
为常数
上关于原点对称的两点，点
是椭圆上的任意一点，若直线
和
的斜率都存在，并分别记为
，
，那么
．类比双曲线
且
，则对于
，
的线段分成
段，每段长度均为正整数，并要求这
段中的任意三段都不能构成三角形．例如，当
时，只可以分为长度分别为1,1,2的三段，此时
时，可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段，此时
时，
时，