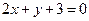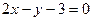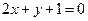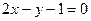题目内容
已知函数f(x)的定义域为[-2,4],且f(4)=f(-2)=1,f′(x)为f(x)的导函数,函数y=f′(x)的图象如下图所示.
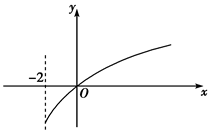
则平面区域所围成的面积是( )

则平面区域所围成的面积是( )
| A.2 | B.4 | C.5 | D.8 |
B
分析:根据导函数的图象,分析原函数的性质或作出原函数的草图,找出a、b满足的条件,画出平面区域,即可求解.
解:由图可知[-2,0)上f′(x)<0,
∴函数f(x)在[-2,0)上单调递减,(0,4]上f′(x)>0,
∴函数f(x)在(0,4]上单调递增,
故在[-2,4]上,f(x)的最大值为f(4)=f(-2)=1,
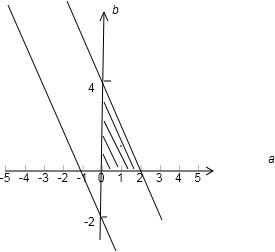
∴f(2a+b)<1(a≥0,b≥0)?
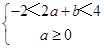
表示的平面区域如图所示:
故选B.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
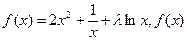 的导数是
的导数是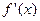 .
.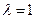 时,
时,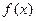 在x=1处的切线方程。
在x=1处的切线方程。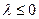 时,求证:对于任意的两个不等的正数
时,求证:对于任意的两个不等的正数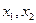 ,有
,有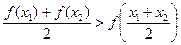 ;
;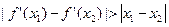 恒成立,求
恒成立,求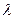 的取值范围.
的取值范围.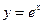 在点A(0,1)处的切线斜率为( )
在点A(0,1)处的切线斜率为( )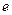
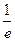
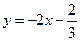 与曲线
与曲线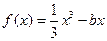 相切。
相切。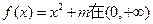 上有两个解
上有两个解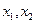 ,求m的取值范围。
,求m的取值范围。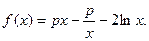
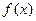 在点(1,
在点(1,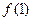 )处的切线方程;
)处的切线方程;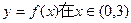 存在极值,求实数P的取值范围。
存在极值,求实数P的取值范围。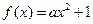 ,若
,若 ,则
,则 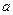 =" " ;
=" " ;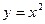 在(1,1)处的切线方程是 ( )
在(1,1)处的切线方程是 ( )