题目内容
【题目】为迎接“五一”节的到来,某单位举行“庆五一,展风采”的活动.现有6人参加其中的一个节目,该节目由![]() 两个环节可供参加者选择,为增加趣味性,该单位用电脑制作了一个选择方案:按下电脑键盘“Enter”键则会出现模拟抛两枚质地均匀骰子的画面,若干秒后在屏幕上出现两个点数
两个环节可供参加者选择,为增加趣味性,该单位用电脑制作了一个选择方案:按下电脑键盘“Enter”键则会出现模拟抛两枚质地均匀骰子的画面,若干秒后在屏幕上出现两个点数![]() 和
和![]() ,并在屏幕的下方计算出
,并在屏幕的下方计算出![]() 的值.现规定:每个人去按“Enter”键,当显示出来的
的值.现规定:每个人去按“Enter”键,当显示出来的![]() 小于
小于![]() 时则参加
时则参加![]() 环节,否则参加
环节,否则参加![]() 环节.
环节.
(1)求这6人中恰有2人参加该节目![]() 环节的概率;
环节的概率;
(2)用![]() 分别表示这6个人中去参加该节目
分别表示这6个人中去参加该节目![]() 两个环节的人数,记
两个环节的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)利用古典概型概率公式得出选择参加![]() 环节的概率
环节的概率![]() ,选择参加
,选择参加![]() 环节的概率
环节的概率![]() ,再利用独立重复实验概率公式,即可得出答案;
,再利用独立重复实验概率公式,即可得出答案;
(2)得出![]() 的可能取值以及对应概率,即可得出分布列以及期望.
的可能取值以及对应概率,即可得出分布列以及期望.
(1)依题意得,由屏幕出现的点数![]() 和
和![]() 形成的有序数对
形成的有序数对![]() ,一共有
,一共有![]() 种等可能的基本事件
种等可能的基本事件
符合![]() 的有
的有![]() ,
,![]() 共24种
共24种
所以选择参加![]() 环节的概率为
环节的概率为![]() ,选择参加
,选择参加![]() 环节的概率为
环节的概率为![]()
所以这6人中恰有2人参加该节目![]() 环节的概率
环节的概率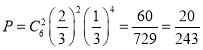
(2)依题意得![]() 的可能取值为
的可能取值为![]()
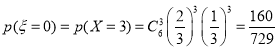
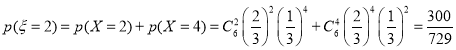
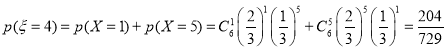

所以![]() 的分布列为
的分布列为
| 0 | 2 | 4 | 6 |
|
|
|
|
|
数学期望![]()

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
【题目】随着我国经济的发展,居民收入逐年增长.某地区2014年至2018年农村居民家庭人均纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
人均纯收入 | 5 | 6 | 7 | 8 | 10 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2014年至2018年该地区农村居民家庭人均纯收入的变化情况,并预测2019年该地区农村居民家庭人均纯收入为多少?
附:回归直线的斜率和截距的最小二乘估计公式分别为 .
.
