题目内容
17.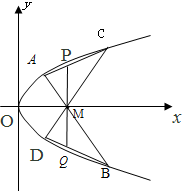 已知抛物线y2=2x上有四点A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),点M(3,0),直线AB、CD都过点M,且都不垂直于x轴,直线PQ过点M且垂直于x轴,交AC于点P,交BD于点Q.
已知抛物线y2=2x上有四点A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),点M(3,0),直线AB、CD都过点M,且都不垂直于x轴,直线PQ过点M且垂直于x轴,交AC于点P,交BD于点Q.(1)求y1y2的值;
(2)求证:MP=MQ.
分析 (1)利用直线AB过点M(3,0)可设直线AB的方程为x=my+3,联立直线与抛物线方程,利用韦达定理可得结论;
(2)利用y2=2x,可得直线AC的斜率为$\frac{{{y_1}-{y_3}}}{{{x_1}-{x_3}}}=\frac{2}{{{y_1}+{y_3}}}$,进而可得直线AC的方程、点P的纵坐标,同理可得点Q的纵坐标,利用PQ⊥x轴即得结论.
解答 (1)解:∵直线AB过点M(3,0),A(x1,y1)、B(x2,y2),
∴设直线AB的方程为x=my+3,
联立方程组$\left\{\begin{array}{l}{x=my+3}\\{{y}^{2}=2x}\end{array}\right.$,得:y2-2my-6=0,
由韦达定理可知y1y2=-6;
(2)证明:∵y2=2x,
∴直线AC的斜率为$\frac{{{y_1}-{y_3}}}{{{x_1}-{x_3}}}=\frac{2}{{{y_1}+{y_3}}}$,
∴直线AC的方程为$y=\frac{2}{{{y_1}+{y_3}}}(x-{x_1})+{y_1}$,
∴点P的纵坐标为${y_P}=\frac{{6+{y_1}{y_3}}}{{{y_1}+{y_3}}}$=$\frac{{6+(-\frac{6}{y_2}){y_3}}}{{-\frac{6}{y_2}+{y_3}}}=\frac{{6({y_2}-{y_3})}}{{{y_2}{y_3}-6}}$,
同理:点Q的纵坐标为yQ=$\frac{{6({y_3}-{y_2})}}{{{y_2}{y_3}-6}}$,
∴yP+yQ=0,
又PQ⊥x轴,
∴MP=MQ.
点评 本题是一道直线与圆锥曲线的综合题,涉及到韦达定理等知识,考查计算能力,注意解题方法的积累,属于中档题.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案| A. | $\frac{32}{3}$,-6 | B. | $\frac{32}{3}$,0 | C. | 6,-$\frac{32}{3}$ | D. | 6,0 |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
(1)若要获利最大年利润,售价应定为多少万元/辆?
(2)该销售店为了提高销售业绩,推出了分期付款的促销活动.已知销售一辆该品牌的汽车,若一次性付款,其利润为2万元;若分2期或3期付款,其利润为2.5万元;若分4期或5期付款,其利润为3万元.该销售店对最近分期付款的10位购车情况进行了统计,统计结果如下表.
| 付款方式 | 一次性 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 1 | 1 | 3 | 2 | 3 |
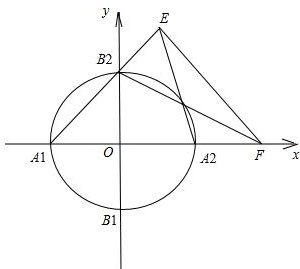 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,直线y=x+$\sqrt{2}$与以原点为圆心、椭圆C的短半轴长为半径的圆O相切.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,直线y=x+$\sqrt{2}$与以原点为圆心、椭圆C的短半轴长为半径的圆O相切.