题目内容
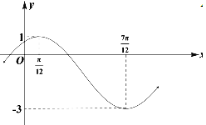
【题目】某心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数p与听课时间t之间的关系满足如图所示的曲线.当t∈(0,14]时,曲线是二次函数图象的一部分,当t∈[14,40]时,曲线是函数![]() (
(![]() 且
且![]() )图象的一部分.根据专家研究,当注意力指数p大于等于80时听课效果最佳.
)图象的一部分.根据专家研究,当注意力指数p大于等于80时听课效果最佳.

(1)试求![]() 的函数关系式;
的函数关系式;
(2)一道数学难题,讲解需要22分钟,问老师能否经过合理安排在学生听课效果最佳时讲完?请说明理由.
【答案】(1)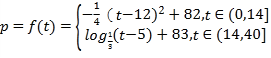 ;(2)能,见解析.
;(2)能,见解析.
【解析】
(1)根据所给的函数图像先求出当t∈(0,14]时的二次函数解析式,再由点![]() ,代入函数
,代入函数![]() 求出t∈[14,40]时的解析式,用分段函数表达即可.
求出t∈[14,40]时的解析式,用分段函数表达即可.
(2)对分段函数,分别解不等式![]() ,求出
,求出![]() 的取值范围,然后取并集,再计算时间的长度,然后对老师能否经过合理安排在学生听课效果最佳时讲完做出判断.
的取值范围,然后取并集,再计算时间的长度,然后对老师能否经过合理安排在学生听课效果最佳时讲完做出判断.
解:(1)当t∈(0,14]时,设p=f(t)=c(t-12)2+82(c<0),
将点(14,81)代入得c=-![]() ,
,
∴当t∈(0,14]时,p=f(t)=-![]() (t-12)2+82;
(t-12)2+82;
当t∈(14,40]时,将点(14,81)代入y=loga(t-5)+83,得a=![]() .
.
所以p=f(t)=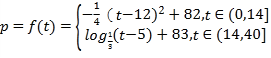
(2)当t∈(0,14]时,- ![]() (t-12)2+82≥80,
(t-12)2+82≥80,
解得:![]() ,
,
所以![]() ;
;
当t∈(14,40]时,log![]() (t-5)+83≥80,
(t-5)+83≥80,
解得5<t≤32,所以t∈(14,32],
综上![]() 时学生听课效果最佳.
时学生听课效果最佳.
此时![]()
所以,教师能够合理安排时间讲完题目.

【题目】利用独立性检验的方法调查高中生的写作水平与离好阅读是否有关,随机询问120名高中生是否喜好阅读,利用2×2列联表,由计算可得K2=4.236
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参照附表,可得正确的结论是( )
A.有95%的把握认为“写作水平与喜好阅读有关”
B.有97.5%的把握认为“写作水平与喜好阅读有关”
C.有95%的把握认为“写作水平与喜好阅读无关”
D.有97.5%的把握认为“写作水平与喜好阅读无关”