题目内容
【题目】已知函数![]() 的部分图象如图所示:
的部分图象如图所示:
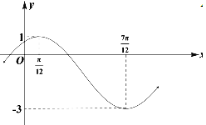
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的单调区间和对称中心坐标;
的单调区间和对称中心坐标;
(3)将![]() 的图象向左平移
的图象向左平移![]() 个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数
个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1)![]() ;(2)
;(2)![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ,
,![]() ;对称中心的坐标为
;对称中心的坐标为![]() ,
,![]() ;(3)最大值
;(3)最大值![]() ,最小值-2.
,最小值-2.
【解析】
(1)由图象可求![]() ,
,![]() 的值,求得周期
的值,求得周期![]() ,利用周期公式可求
,利用周期公式可求![]() ,由
,由![]() 可求
可求![]() ,即可得解
,即可得解![]() 的解析式;
的解析式;
(2)令![]() ,
,![]() ,得
,得![]() ,
,![]() ,可求
,可求![]() 的单调递增区间,令
的单调递增区间,令![]() ,
,![]() ,得
,得![]() ,
,![]() ,可求
,可求![]() 的对称中心的坐标;
的对称中心的坐标;
(3)由已知的图象变换过程可得:![]() ,由
,由![]() ,利用正弦函数的性质可求在
,利用正弦函数的性质可求在![]() 上的最大值和最小值.
上的最大值和最小值.
(1)由图象可知![]() ,
,
解得![]() ,
,
又由于![]() ,
,
所以![]() ,
,
由![]() ,
,
![]() ,
,
又![]() ,
,
所以![]() ,
,
所以![]() ;
;
(2)由(1)知,![]() ,
,
令![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,
所以![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() ,
,
令![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
所以![]() 的对称中心的坐标为
的对称中心的坐标为![]() ,
,![]() ;
;
(3)由已知的图象变换过程可得:![]() ,
,
因为![]() ,
,
所以![]() ,
,
所以当![]() ,得
,得![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
当![]() 时,即
时,即![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】在测试中,客观题难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
| 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
(Ⅰ)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;
题号 | 1 | 2 | 3 | 4 | 5 |
实测答对人数 | |||||
实测难度 |
(Ⅱ)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(Ⅲ)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度, ![]() 为第
为第![]() 题的预估难度
题的预估难度![]() .规定:若
.规定:若![]() ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
【题目】第一次大考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于![]() 分为优秀,
分为优秀,![]() 分以下为非优秀,统计成绩后,得到如下
分以下为非优秀,统计成绩后,得到如下![]() 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部![]() 人中随机抽取
人中随机抽取![]() 人为优秀的概率为
人为优秀的概率为![]() .
.
(I)请完成![]() 列联表:
列联表:
优秀 | 非优秀 | 合计 | |
甲班 |
| ||
乙班 |
| ||
合计 |
|
(Ⅱ)根据列联表的数据能否在犯错误的概率不超过![]() 的前提下认为成绩与班级有关系?
的前提下认为成绩与班级有关系?
参考公式和临界值表:
 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|