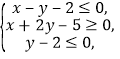Question

【题目】选修4-5：不等式选讲

已知函数.

（1）求不等式的解集；

（2）若不等式的解集非空，求的取值范围.

Answer 1

【答案】（1）（2）

【解析】分析：（1）求出的分段函数的形式，解不等式可分与，三类讨论即可解得不等式的解集；

（2）原式等价于存在，使成立，即 ，

设，求出的最大值即可得到的取值范围.

详解：（1）当时，，无解

当时， ∴

当时，

综上所述的解集为 .

（2）原式等价于存在，使

成立，即

设

由（1）知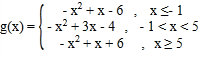

当时，，其开口向下，对称轴为x=>-1,所以g(x)≤g(-1)=-8,

当-1<x<5,开口向下，对称轴x=,所以g(x)≤g()=-

当x≥5时，开口向下，对称轴x=<5，所以g(x)≤g(5)=-14，

综上所述，t的取值范围为（-∞，-].