Question

4．下列命题中正确的个数是（　　）
①过异面直线a，b外一点P有且只有一个平面与a，b都平行；
②异面直线a，b在平面α内的射影相互垂直，则a⊥b；
③底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；
④直线a，b分别在平面α，β内，且a⊥b，则α⊥β．

• A． 0
• B． 1
• C． 2
• D． 3

Answer 1

分析 列举反例，即可得出结论．

解答 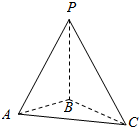解：①P是异面直线a、b外一点，则过P有一个平面与a、b都平行；此命题不正确，当过点P与两条异面直线中的一条的平面与另一条直线平行时，此时找不到一个过P的平面与两条异面直线都平行，不正确；
②本命题用图形说明，如图：

三棱锥P-ABC中，侧棱PB垂直于底面，PA，PC两线在底面上的投影垂直，而两线不垂直，不正确；
③四边相等的四边形也可以是空间四边形，不正确；
④直线a，b分别在平面α，β内，且a⊥b，则α、β不一定垂直，不正确．
故选：A．

点评 本题考查命题真假的判断，考查了空间中线线位置关系，线面位置关系，两异面直线的关系等，正确解答本题，关键是要有着较好的空间立体感知能力，能对命题所涉及的问题找到恰当的模型做载体进行判断．本题是训练空间感知能力的一道好题．