题目内容
已知函数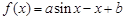 (a,b均为正常数).
(a,b均为正常数).
(1)求证:函数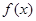 在
在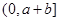 内至少有一个零点;
内至少有一个零点;
(2)设函数在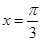 处有极值,
处有极值,
①对于一切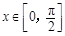 ,不等式
,不等式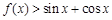 恒成立,求
恒成立,求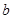 的取值范围;
的取值范围;
②若函数f(x)在区间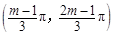 上是单调增函数,求实数
上是单调增函数,求实数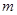 的取值范围.
的取值范围.
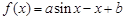 (a,b均为正常数).
(a,b均为正常数). (1)求证:函数
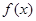 在
在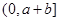 内至少有一个零点;
内至少有一个零点;(2)设函数在
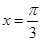 处有极值,
处有极值,①对于一切
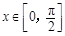 ,不等式
,不等式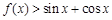 恒成立,求
恒成立,求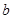 的取值范围;
的取值范围;②若函数f(x)在区间
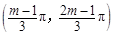 上是单调增函数,求实数
上是单调增函数,求实数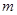 的取值范围.
的取值范围. (1)详见解析;(Ⅱ)①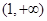 ②
②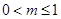 .
.
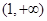 ②
②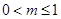 .
.试题分析:(Ⅰ)证明函数
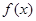 在
在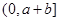 内至少有一个零点,可由零点的存在性定理考察
内至少有一个零点,可由零点的存在性定理考察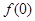 和
和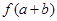 的符号,若
的符号,若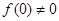 且
且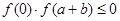 ,则结论成立,若
,则结论成立,若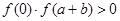 ,可将区间
,可将区间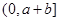 进行适当分割,再依上面方法进行,直到找到函数的零点的存在区间;(Ⅱ)易知
进行适当分割,再依上面方法进行,直到找到函数的零点的存在区间;(Ⅱ)易知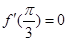 ,从而求出
,从而求出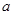 的值.
的值.①不等式
 恒成立可化分离参数转化为求函数在区间
恒成立可化分离参数转化为求函数在区间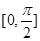 上的最值问题,这是一个普通的三角函数问题,通过判断三角函数的单调性容易解决;②函数在一个已知区间上为增函数,求参数的取值范围问题,通常有两种方法,一是用在这个区间上导函数的符号确定,一般三角函数不用此方法,二是求出函数的单调递增区间,它必包含已知区间,然后考察参数的取值范围.
上的最值问题,这是一个普通的三角函数问题,通过判断三角函数的单调性容易解决;②函数在一个已知区间上为增函数,求参数的取值范围问题,通常有两种方法,一是用在这个区间上导函数的符号确定,一般三角函数不用此方法,二是求出函数的单调递增区间,它必包含已知区间,然后考察参数的取值范围.试题解析:(1)证明:
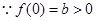 ,
,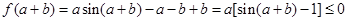
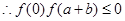
所以,函数
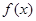 在
在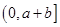 内至少有一个零点 4分
内至少有一个零点 4分(2)
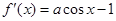 由已知得:
由已知得: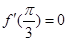 所以a=2,
所以a=2,所以
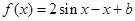 5分
5分①不等式
 恒成立可化为:
恒成立可化为: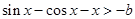
记函数
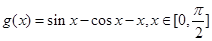
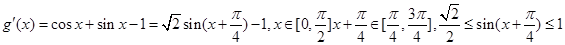
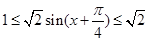 ,所以
,所以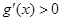 在
在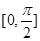 恒成立 8分
恒成立 8分函数
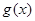 在
在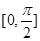 上是增函数,最小值为
上是增函数,最小值为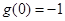
所以
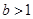 , 所以
, 所以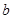 的取值范围是
的取值范围是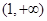 10分
10分②由
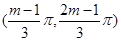 得:
得: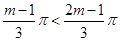 ,所以
,所以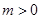 11分
11分令
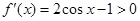 ,可得
,可得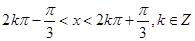 13分
13分∵函数
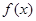 在区间(
在区间(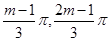 )上是单调增函数,
)上是单调增函数,∴
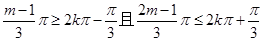 14分
14分∴
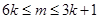 ,
,∵
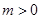 ,∴
,∴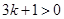 ,
,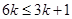 ∴
∴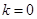 ∴
∴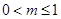 16分
16分
练习册系列答案
相关题目
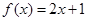 ,
,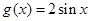 ,则
,则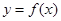 与
与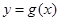 图像在区间
图像在区间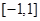 内交点的个数为( )
内交点的个数为( )
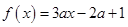 在
在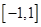 上存在一个零点,则
上存在一个零点,则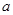 的取值范围是: ( )
的取值范围是: ( )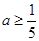
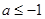

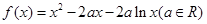 ,则下列说法不正确的是( )
,则下列说法不正确的是( )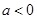 时,函数
时,函数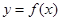 有零点
有零点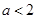
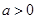 ,函数
,函数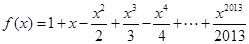 且函数
且函数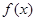 的零点均在区间
的零点均在区间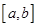
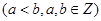 内,圆
内,圆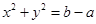 的面积的最小值是( )
的面积的最小值是( )
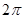
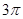
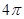
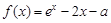 在
在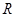 上有两个零点,则实数
上有两个零点,则实数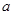 的取值范围是________.
的取值范围是________.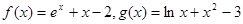 ,若实数
,若实数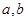 满足
满足 ,则( )
,则( )



 的解是 .
的解是 .