题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点. 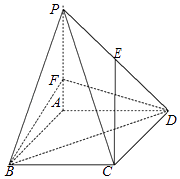
(Ⅰ)若 AF=1,求证:CE∥平面 BDF;
(Ⅱ)若 AF=2,求平面 BDF 与平面 PCD所成的锐二面角的余弦值.
【答案】解:(Ⅰ)证明:如图所示,取PF中点G,连接EG,CG.
连接AC交BD于O,连接FO.
由题可得F为AG中点,O为AC中点,
∴FO∥GC;
又G为PF中点,E为PD中点,
∴GE∥FD.
又GE∩GC=G,GE、GC面GEC,
FO∩FD=F,FO,FD面FOD.
∴面GEC∥面FOD.
∵CE面GEC,
∴CE∥面BDF;

(Ⅱ)解:∵底面ABCD是边长为 3 的菱形,
∴AC⊥BD,设交点为O,以O为坐标原点建立如图所示空间直角坐标系,
则B(0,﹣ ![]() ,0),D(0,
,0),D(0, ![]() ,0),P(﹣
,0),P(﹣ ![]() ,0,3),C(
,0,3),C( ![]() ,0,0),F(
,0,0),F( ![]() ,0,2).
,0,2).
则 ![]() ,
,  ,
, 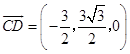 ,
,  .
.
设平面BDF的一个法向量为 ![]() ,
,
则  ,取z=3,得
,取z=3,得 ![]() .
.
设平面PCD的一个法向量为 ![]() ,
,
则  ,取y=
,取y= ![]() ,得
,得 ![]() .
.
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
∴平面 BDF 与平面 PCD所成的锐二面角的余弦值为 ![]() .
.

【解析】(Ⅰ)取PF中点G,连接EG,CG.连接AC交BD于O,连接FO.由三角形中位线定理可得FO∥GC,GE∥FD.然后利用平面与平面平行的判定得到面GEC∥面FOD,进一步得到CE∥面BDF;(Ⅱ)由底面ABCD是边长为 3 的菱形,可得AC⊥BD,设交点为O,以O为坐标原点建立如图所示空间直角坐标系,求出所用点的坐标,再求出平面 BDF 与平面 PCD的一个法向量,由两法向量所成角的余弦值求得平面 BDF 与平面 PCD所成的锐二面角的余弦值.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行).

【题目】某汽车的使用年数x与所支出的维修费用y的统计数据如表:
使用年数x(单位:年) | 1 | 2 | 3 | 4 | 5 |
维修总费用y(单位:万元) | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
根据上表可得y关于x的线性回归方程 ![]() =
= ![]() x﹣0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
x﹣0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
A.8年
B.9年
C.10年
D.11年


