题目内容

（2013•东莞二模）（几何证明选讲选做题）
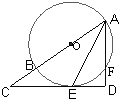
如图所示，AB是⊙O的直径，过圆上一点E作切线ED⊥AF，交AF的延长线于点D，交AB的延长线于点C．若CB=2，CE=4，则AD的长为
24
5
24
5
．
分析：设出圆的半径直接利用切割线定理求出圆的半径，通过三角形相似列出比例关系求出AD即可．
解答：解：设r是⊙O的半径．由切割线定理可知：CE2=CA•CB，
即42=（2r+2）×2，解得r=3．
因为EC是圆的切线，所以OE⊥EC，AD⊥DC，
所以△ADC∽△OEC，所以
CO
CA
=
OE
AD
，
5
8
=
3
AD
，
解得AD=
24
5
．
故答案为：
24
5
．
点评：本题考查圆的切割线定理的应用，三角形相似的证明以及应用，考查计算能力．
练习册系列答案
相关题目
（2013•东莞二模）设Sn为数列{an}前n项和，对任意的n∈N*，都有Sn=2-an，数列{bn}满足bn=
bn-1
1+bn-1
，b1=2a1，
（1）求证：数列{an}是等比数列，并求{an}的通项公式；
（2）求数列{bn}的通项公式；
（3）求数列{
1
an+2bn
}的前n项和Tn．
（2013•东莞二模）命题“?x∈R，x2+1≥1”的否定是（　　）
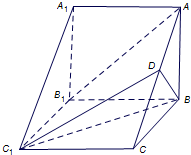（2013•东莞二模）如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1=AB=2．
（1）求证：AB1∥平面BC1D；
（2）若BC=3，求三棱锥D-BC1C的体积．
（2013•东莞二模）已知x＞0，y＞0，且
1
x
+
9
y
=1，则2x+3y的最小值为
29+6
6
29+6
6
．
（2013•东莞二模）已知函数f(x)=tan(
1
3
x-
π
6
)
（1）求f（x）的最小正周期；
（2）求f(
3π
2
)的值；
（3）设f(3α+
7π
2
)=-
1
2
，求
sin(π-α)+cos(α-π)
2
sin(α+
π
4
)
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网